
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
(1)计算:2sin30°+3﹣1+(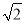 ﹣1)0-
﹣1)0-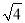 ;
;
(2)计算: 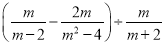 .
.
查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
(1)解方程:x2+4x﹣1=0;
(2)解不等式组: 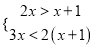 .
.
查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
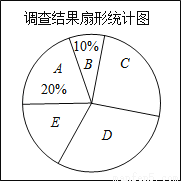
2014年全国两会民生话题成为社会焦点.合肥市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了合肥市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
组别 | 焦点话题 | 频数(人数) |
A | 食品安全 | 80 |
B | 教育医疗 | m |
C | 就业养老 | n |
D | 生态环保 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= .扇形统计图中E组所占的百分比为 %;
(2)合肥市人口现有750万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B 布袋中有三个完全相同的小球,分别标有数字﹣1,﹣2和﹣3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=﹣x﹣1上的概率.
(1)见解析;(2) 【解析】试题分析: (1)由题意用列表法列出所有等可能事件如下,即可得到点Q所有可能的坐标; (2)把所有可能的点Q的坐标代入解析式检验即可得到点Q落在直线上的有几种,由此即可得到点Q落在直线是的概率. 试题解析: (1)列表如下,表中坐标为点Q所有可能的坐标: 1 2 ﹣1 (1,﹣1) (2,﹣1) ...查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
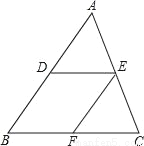
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
(1)见解析;(2) AB=BC 【解析】试题分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,然后根据两组对边分别平行的四边形是平行四边形证明. (2)根据邻边相等的平行四边形是菱形证明. 试题解析: (1)∵D、E分别是AB、AC的中点, ∴DE是△ABC的中位线. ∴DE∥BC. 又∵EF∥AB, ∴四边形DBFE是...查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
(1)y=2x+2(2)15km 【解析】(1)根据函数图象可以得出出租车的起步价是8元,设当x>3时,y与x之间的甬数解析式为y=kx+b(k≠0),运用待定系数法就可以得出结论; (2)将y=32代入(1)中的解析式就可以求出x的值.查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
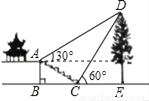
某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)
查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
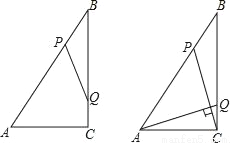
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
(1) t=1或 ;(2) 【解析】试题分析: (1)由∠B是△BPQ与△ABC的公共角,可知,若两三角形相似,存在两种情况:①△BPQ∽△BAC;②△BPQ∽△BCA;分这两种情况结合相似三角形的性质和题意即可解得对应的t的值; (2)如图1,过P作PM⊥BC于点M,AQ,CP交于点N,由题意可知:当AQ⊥CP时,△ACQ∽△CMP,由相似三角形的性质列出比例式即可解得对应的t...查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
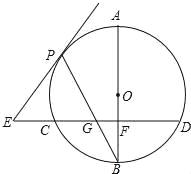
(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG2=BFBO.试证明BG=PG;
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB=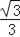 .求弦CD的长.
.求弦CD的长.
查看答案和解析>>
科目: 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
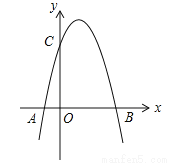
如图,二次函数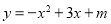 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com