
科目: 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
解方程: 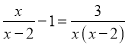 .
.
查看答案和解析>>
科目: 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
先化简,再求值: 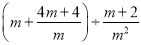 ,其中
,其中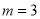 .
.
查看答案和解析>>
科目: 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
如图,A,B分别为CD,CE的中点,AE⊥CD于点A,BD⊥CE于点B.求∠AEC的度数.
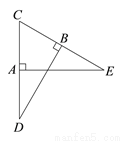
查看答案和解析>>
科目: 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”,是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化,某校为各班购进《三国演义》和《水浒传》连环画若干套,其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元,用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍,求每套《水浒传》连环画的价格.
每套《水浒传》连环画的价格为120元 【解析】试题分析:设每套《水浒传》连环画的价格为x元,则每套《三国演义》连环画的价格为(x+60)元,根据等量关系“用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍”列方程进行求解即可得. 试题解析:设每套《水浒传》连环画的价格为元,则每套《三国演义》连环画的价格为元, 由题意,得, 解得, 经...查看答案和解析>>
科目: 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
阅读材料
小明遇到这样一个问题:求计算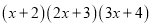 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算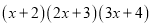 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找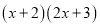 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:
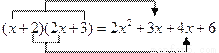
也就是说,只需用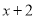 中的一次项系数1乘以
中的一次项系数1乘以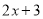 中的常数项3,再用
中的常数项3,再用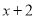 中的常数项2乘以
中的常数项2乘以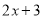 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加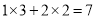 ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算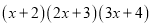 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用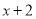 的一次项系数1,
的一次项系数1, 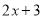 的常数项3,
的常数项3, 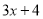 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用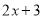 的一次项系数2,
的一次项系数2, 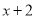 的常数项2,
的常数项2, 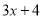 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用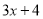 的一次项系数3,
的一次项系数3, 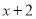 的常数项2,
的常数项2, 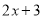 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算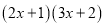 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算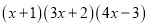 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算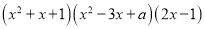 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则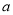 =_________.
=_________.
(4)若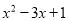 是
是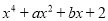 的一个因式,则
的一个因式,则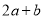 的值为 .
的值为 .
查看答案和解析>>
科目: 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
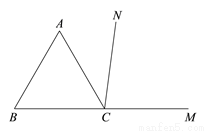
如图,CN是等边△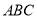 的外角
的外角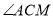 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若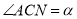 ,求
,求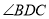 的大小(用含
的大小(用含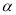 的式子表示);
的式子表示);
(3)用等式表示线段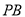 ,
, 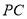 与
与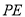 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目: 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:
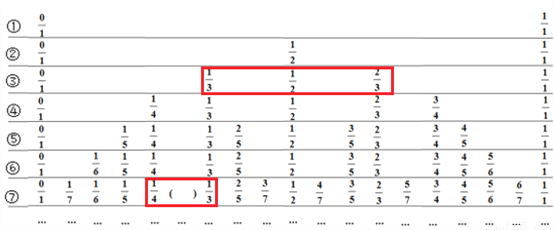
两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数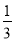 、
、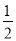 、
、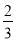 ,有
,有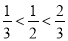 ,所以
,所以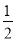 为
为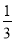 和
和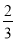 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到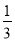 和
和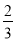 的中间分数
的中间分数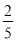 ,
, 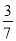 ,
, 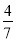 ,
, 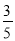 .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到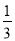 和
和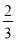 更多的中间分数.
更多的中间分数.
(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的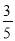 和
和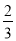 的中间分数是 ;
的中间分数是 ;
(2)写出分数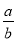 和
和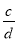 (a、b、c、d均为正整数,
(a、b、c、d均为正整数, 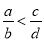 ,
, 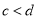 )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;
(3)若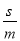 与
与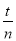 (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是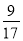 和
和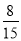 的中间分数,则
的中间分数,则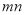 的最小值为 .
的最小值为 .
查看答案和解析>>
科目: 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
下列图案:

其中,中心对称图形是( )
A.①② B.②③ C. ②④ D.③④
D 【解析】 试题分析:根据中心对称图形的概念:绕某点旋转180°,能够与原图形完全重合的图形.可知①不是中心对称图形;②不是中心对称图形;③是中心对称图形;④是中心对称图形. 故选:D.查看答案和解析>>
科目: 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
一元二次方程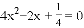 的根的情况是( )
的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 无法判断
C 【解析】∵在方程中,, ∴△=, ∴原方程有两个相等的实数根. 故选B.查看答案和解析>>
科目: 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
抛物线y=2x2-12x+22 的顶点是( )
A. (3,-4) B. (-3,4) C. (3,4) D. (2,4)
C 【解析】∵, ∴抛物线的顶点坐标为(3,4). 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com