
科目: 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
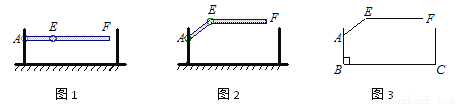
某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
查看答案和解析>>
科目: 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
如图,⊙O是△ABC的外接圆,AB=AC,P是⊙O上一点.
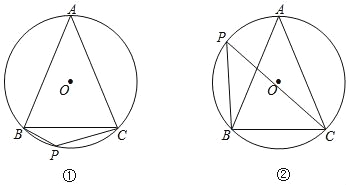
(1)操作:请你只用无刻度的直尺,分别画出图①和图②中∠P的平分线;
(2)说理:结合图②,说明你这样画的理由.
(1)图见解析;(2)理由见解析. 【解析】 试题分析:(1)图①中,连接AP即为∠P的平分线;图②中,连接AO交⊙O于点E,连接PE即为∠P的平分线;(2)根据等弧所对的圆周角相等即可得出结论. 试题解析:(1)如图①,AP即为∠P的平分线;图②中,连接PE即为∠P的平分线; (2)如图②,∵AB=AC, ∴AE是BA的垂直平分线, ∴= , ∴∠BPE...查看答案和解析>>
科目: 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高1元其销售量就减少20件.
(1)当售价定为12元时,每天可售出 件;
(2)要使每天利润达到640元,则每件售价应定为多少元?
(3)当每件售价定为多少元时,每天获得最大利润?并求出最大利润.
(1) 160;(2) 当每件售价定为14元时,每天获得最大利润为720元. 【解析】试题分析:(1)由原来的销量﹣减少的销量就可以得出现在的销量而得出结论;(2)由利润=每件利润×销售数量建立方程求出其解即可;(3)设每天获得的利润为W元,由利润=每件利润×销售数量建立W与x的关系式,由二次函数的性质就可以求出结论. 试题解析:(1)由题意,得 200﹣20×(12﹣10)=1...查看答案和解析>>
科目: 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+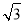 ,BC=2
,BC=2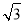 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目: 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
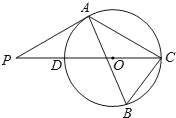
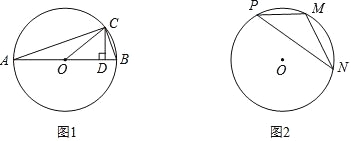
【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα=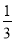 ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=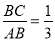 ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
【问题解决】
(1)请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ=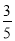 ,求sin2β的值.
,求sin2β的值.
查看答案和解析>>
科目: 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
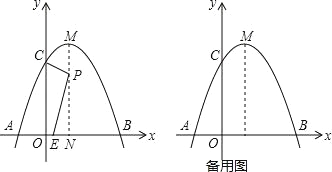
如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.
查看答案和解析>>
科目: 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:单选题
关于x的一元二次方程x2+a2﹣1=0的一个根是0,则a的值为( )
A. ﹣1 B. 1 C. 1或﹣1 D. 3
C 【解析】由题意可得: ,解得. 故选C.查看答案和解析>>
科目: 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:单选题
已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )
A. 相交 B. 相切 C. 相离 D. 不能确定
A 【解析】∵O的半径为3,圆心O到直线L的距离为2, ∵3>2,即:d查看答案和解析>>
科目: 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:单选题
一元二次方程3x2﹣6x+4=0根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 有两个实数根
C 【解析】∵在方程3x2﹣6x+4=0中,a=3,b=-6,c=4, ∴△=, ∴原方程没有实数根. 故选C.查看答案和解析>>
科目: 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:单选题
向如图所示的地砖上随机地掷一个小球,当小球停下时,最终停在地砖上阴影部分的概率是( )

A. 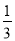 B.
B. 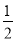 C.
C. 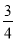 D.
D. 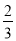
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com