
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:填空题
已知抛物线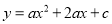 ,那么点P(-3,4)关于该抛物线的对称轴对称的点的坐标是______.
,那么点P(-3,4)关于该抛物线的对称轴对称的点的坐标是______.
查看答案和解析>>
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:填空题
在平面直角坐标系中,将点(-b,-a)称为点(a,b)的“关联点”(例如点(-2,-1)是点(1,2)的“关联点”).如果一个点和它的“关联点”在同一象限内,那么这一点在第_______象限.
二、四. 【解析】试题解析:根据关联点的特征可知: 如果一个点在第一象限,它的关联点在第三象限. 如果一个点在第二象限,它的关联点在第二象限. 如果一个点在第三象限,它的关联点在第一象限. 如果一个点在第四象限,它的关联点在第四象限. 故答案为:二,四.查看答案和解析>>
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:填空题
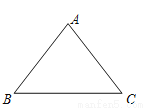
如图,在△ABC中,AB=AC,将△ABC绕点A旋转,当点B与点C重合时,点C落在点D处,如果sinB=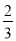 ,BC=6,那么BC的中点M和CD的中点N的距离是_______
,BC=6,那么BC的中点M和CD的中点N的距离是_______
查看答案和解析>>
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:解答题
已知:如图,Rt△ABC中,∠ACB=90°,sinB=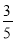 ,点D、E分别在边AB、BC上,且AD∶DB=2∶3,DE⊥BC.
,点D、E分别在边AB、BC上,且AD∶DB=2∶3,DE⊥BC.
(1)求∠DCE的正切值;
(2)如果设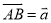 ,
, 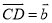 ,试用
,试用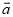 、
、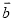 表示
表示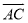 .
.
查看答案和解析>>
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:解答题
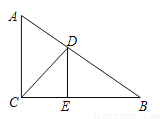
甲、乙两人分别站在相距6米的A、B两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面1米的C处发出一球,乙在离地面1.5米的D处成功击球,球飞行过程中的最高点H与甲的水平距离AE为4米,现以A为原点,直线AB为x轴,建立平面直角坐标系(如图所示).求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度.
查看答案和解析>>
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:解答题
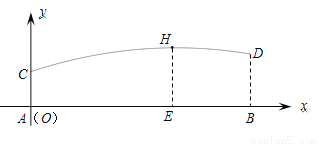
如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
查看答案和解析>>
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:解答题
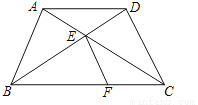
已知:梯形ABCD中,AD//BC,AD=AB,对角线AC、BD交于点E,点F在边BC上,且∠BEF=∠BAC.
(1)求证:△AED∽△CFE;
(2)当EF//DC时,求证:AE=DE.
查看答案和解析>>
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:解答题
在平面直角坐标系xOy中,抛物线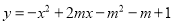 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线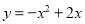 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;
(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
查看答案和解析>>
科目: 来源:2017学年度第一学期上海(杨浦区)期末考试初三数学试卷 题型:解答题
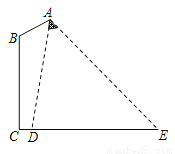
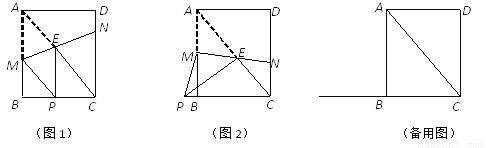
已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com