
科目: 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
先化简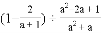 ,再从
,再从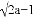 有意义的范围内选取一个整数作为a的值代入求值.
有意义的范围内选取一个整数作为a的值代入求值.
查看答案和解析>>
科目: 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
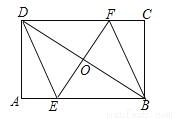
如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目: 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
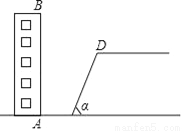
(2017贵州黔东南州第22题)如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81, 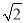 ≈1.41,
≈1.41, 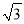 ≈1.73,
≈1.73, 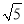 ≈2.24)
≈2.24)
查看答案和解析>>
科目: 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
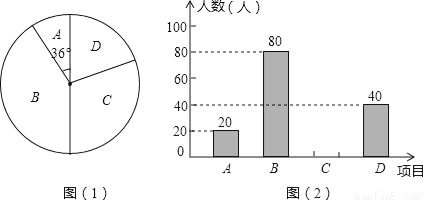
某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目: 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
(8分)已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.
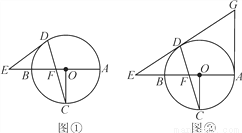
(1)如图①,求证:ED为⊙O的切线;
(2)如图②,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.
(1)见解析;(2)12 【解析】试题分析:(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线; (2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余...查看答案和解析>>
科目: 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
(1)y1=2x(x≥0);y2=x2(x≥0);(2)他至少获得14万元利润,他能获取的最大利润是32万元;(3)6≤m≤8. 【解析】试题分析:(1)根据题意设y1=kx、y2=ax2,将表格中数据分别代入求解可得; (2)由种植花卉m万元(0≤m≤8),则投入种植树木(8-m)万元,根据“总利润=花卉利润+树木利润”列出函数解析式,利用二次函数的性质求得最值即可; (3)根据获利不...查看答案和解析>>
科目: 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
(10分)已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF、CF.
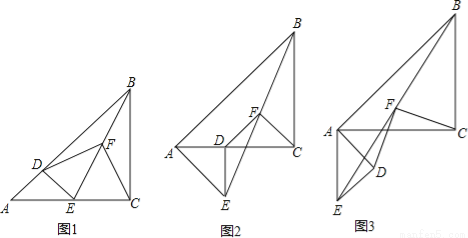
(1)如图1, 当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=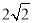 ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
查看答案和解析>>
科目: 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
已知二次函数y=ax2+bx-2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=-2和x=5时二次函数的函数值y相等.
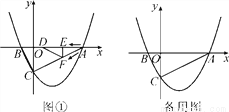
(1)求实数a,b的值;
(2)如图①,动点E,F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒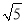 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由;
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式.
(1), ;(2)①t=或t= ,②. 【解析】试题分析:(1)根据抛物线图象经过点A以及“当x=﹣2和x=5时二次函数的函数值y相等”两个条件,列出方程组求出待定系数的值. (2)①首先由抛物线解析式能得到点A、B、C三点的坐标,则线段OA、OB、OC的长可求,进一步能得出AB、BC、AC的长;首先用t 表示出线段AD、AE、AF(即DF)的长,则根据AE、EF、OA、OC的长以及公...查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(遵义):期中检测题 题型:单选题
9的算术平方根是( )
A. ﹣3 B. ±3 C. 3 D. 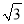
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(遵义):期中检测题 题型:单选题
在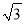 ,
, 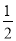 ,0,-2这四个数中,为无理数的是( )
,0,-2这四个数中,为无理数的是( )
A. 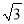 B.
B. 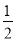 C. 0 D. -2
C. 0 D. -2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com