
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:填空题
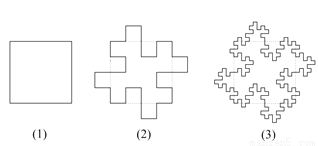
在某多媒体电子杂志的某一期上刊登了“正方形雪花图案的形成”的演示案例:作一个正方形,设每边长为4a,将每边四等分,作一凸一凹的两个边长为a的小正方形,得到图形如图(2)所示,称为第一次变化,再对图(2)的每个边做相同的变化,得到图形如图(3),称为第二次变化.如此连续作几次,便可得到一个绚丽多彩的雪花图案.如不断发展下去到第n次变化时,图形的面积是否会变化,________(填写“会”或者“不会”),图形的周长为__________.
查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
计算:
(1)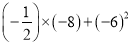 ;(2)
;(2)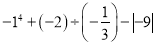 .
.
查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
解方程:
(1)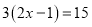 ;(2)
;(2)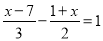 .
.
查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
已知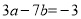 ,求代数式
,求代数式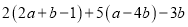 的值.
的值.
查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
作图题:
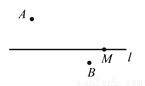
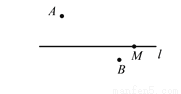
如图,已知点A,点B,直线l及l上一点M.
(1)连接MA,并在直线l上作出一点N,使得点N在点M的左边,且满足MN=MA;
(2)请在直线l上确定一点O,使点O到点A与点O到点B的距离之和最短,并写出画图的依据.
查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
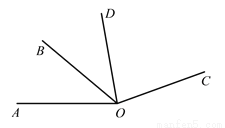
几何计算:
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=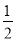 __________=__________°
__________=__________°
查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
如图1,线段AB=10,点C,E,F在线段AB上.

(1)如图2,当点E,点F是线段AC和线段BC的中点时,求线段EF的长;
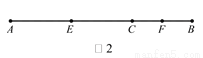
(2)当点E,点F是线段AB和线段BC的中点时,请你写出线段EF与线段AC之间的数量关系并简要说明理由.

查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
先阅读,然后答题.
阿基米德测皇冠的故事
叙古拉国王艾希罗交给金匠一块黄金,让他做一顶王冠.王冠做成后,国王拿在手里觉得有点轻.他怀疑金匠掺了假,可是金匠以脑袋担保说没有,并当面拿秤来称,结果与原来的金块一样重.国王还是有些怀疑,可他又拿不出证据,于是把阿基米德叫来,要他来解决这个难题.回家后,阿基米德闭门谢客,冥思苦想,但百思不得其解.一天,他的夫人逼他洗澡.当他跳入池中时,水从池中溢了出来.阿基米德听到那哗哗哗的流水声,灵感一下子冒了出来.他从池中跳出来,连衣服都没穿,就冲到街上,高喊着:"优勒加!优勒加!(意为发现了)".夫人这回可真着急了,嘴里嘟囔着"真疯了,真疯了",便随后追了出去.街上的人不知发生了什么事,也都跟在后面追着看.原来,阿基米德由澡盆溢水找到了解决王冠问题的办法:相同质量的相同物质泡在水里,溢出的水的体积应该相同.如果把王冠放到水了,溢出的水的体积应该与相同质量的金块的体积相同,否则王冠里肯定掺有假.阿基为德跑到王宫后立即找来一盆水,又找来同样重量的一块黄金,一块白银,分两次泡进盆里,白银溢出的水比黄金溢出的几乎要多一倍,然后他又把王冠和金块分别泡进水盆里,王冠溢出的水比金块多,显然王冠的质量不等于金块的质量,王冠里肯定掺了假.在铁的事实面前,金匠不得不低头承认,王冠里确实掺了白银.烦人的王冠之谜终于解开了.
小明受阿基米德测皇冠的故事的启发,想要做以下的一个探究:
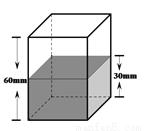
小明准备了一个长方体的无盖容器和A,B两种型号的钢球若干.先往容器里加入一定量的水,如图,水高度为30mm,水足以淹没所有的钢球.
探究一:小明做了两次实验,先放入3个A型号钢球,水面的高度涨到36mm;把3个A型号钢球捞出,再放入2个B型号钢球,水面的高度恰好也涨到36mm.
由此可知A型号与B型号钢球的体积比为____________;
探究二:小明把之前的钢球全部捞出,然后再放入A型号与B型号钢球共10个后,水面高度涨到57mm,问放入水中的A型号与B型号钢球各几个?
查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
(1)-5;(2)1;(3)k=1,﹣1,﹣2,﹣4. 【解析】试题分析:利用定义的新运算,分别列式或者列方程计算. 试题解析: 解:(1)﹣5…………………….. (2)1 ……………………..4分 (3)∵等式(-3,2x-1)★(k,x+k)=5+2k的x是整数, ∴(2x﹣1)k﹣(﹣3)(x﹢k)=5﹢2k, ∴(2k﹢3)x=5, ∴, ...查看答案和解析>>
科目: 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:解答题
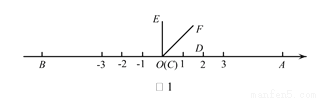
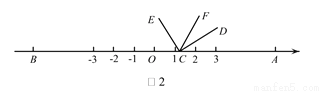
如图1,在数轴上A,B两点对应的数分别是6,-6, 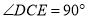 (C与O重合,D点在数轴的正半轴上)
(C与O重合,D点在数轴的正半轴上)
(1)如图1,若CF 平分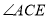 ,则
,则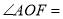 _________;
_________;
(2)如图2,将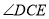 沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点
沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点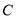 逆时针旋转30t度,作
逆时针旋转30t度,作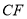 平分
平分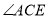 ,此时记
,此时记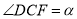 .
.
①当t=1时, 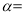 _______;
_______;
②猜想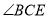 和
和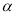 的数量关系,并证明;
的数量关系,并证明;
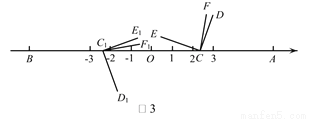
(3)如图3,开始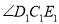 与
与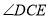 重合,将
重合,将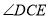 沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点
沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点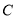 逆时针旋转30t度,作
逆时针旋转30t度,作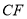 平分
平分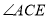 ,此时记
,此时记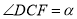 ,与此同时,将
,与此同时,将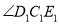 沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点
沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点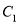 顺时针旋转30t度,作
顺时针旋转30t度,作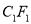 平分
平分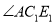 ,记
,记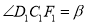 ,若
,若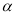 与
与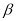 满足
满足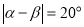 ,请直接写出t的值为_________.
,请直接写出t的值为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com