
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:填空题
在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离.如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾x m,若大巴车车顶高于小张的水平视线0.8m,红灯下沿高于小张的水平视线3.2m,若小张能看到整个红灯,则x的最小值为__________.

查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:填空题
下面是“作一个30°角”的尺规作图过程.

请回答:该尺规作图的依据是______________________________________________________.
三条边相等的三角形是等边三角形,等边三角形的三个内角都是60°,一条弧所对的圆周角是它所对圆心角的一半;或:直径所对的圆周角为直角,三条边相等的三角形是等边三角形,等边三角形的三个内角都是60°,直角三角形两个锐角互余;或:直径所对的圆周角为直角, , 为锐角, . 【解析】连接OD,CD,因为OC=OC=CD,所以OCD是等边三角形,∠A= 三条边相等的三角形是等边三角形,等边三角形...查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
计算: 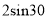 °
°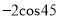 °
°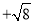 .
.
查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
已知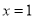 是关于x的方程
是关于x的方程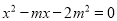 的一个根,求
的一个根,求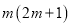 的值.
的值.
查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
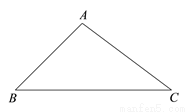
如图,在△ABC中,∠B为锐角, AB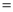
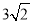 ,AC
,AC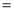 5,
5, 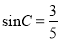 ,求BC的长.
,求BC的长.
查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.轮船到达目的地后开始卸货,记平均卸货速度为v(单位:吨/天),卸货天数为t.
(1)直接写出v关于t的函数表达式:v= ;(不需写自变量的取值范围)
(2)如果船上的货物5天卸载完毕,那么平均每天要卸载多少吨?
(1);(2)平均每天要卸载48吨. 【解析】试题分析: (1)由已知可得轮船上共有货物30×8=240吨,由此可得: ; (2)把代入(1)中所得函数关系式,即可求得平均每天要卸载的货物吨数. 试题解析: (1)由题意可得 : ,即答案为: ; (2)由题意,当时, . 答:平均每天要卸载48吨.查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
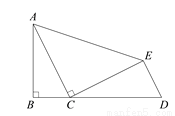
如图,在△ABC中,∠B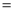 90°,AB
90°,AB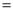 4,BC
4,BC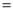 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE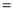 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD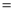 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.
查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中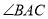 为锐角,图2中
为锐角,图2中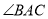 为直角,图3中
为直角,图3中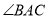 为钝角).
为钝角).
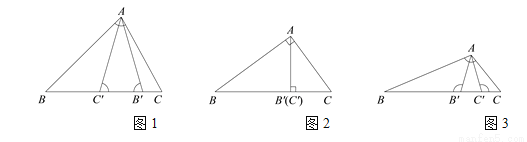
在△ABC的边BC上取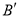 ,
, 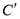 两点,使
两点,使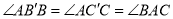 ,则
,则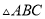 ∽
∽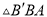 ∽
∽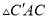 ,
, 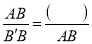 ,
, 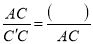 ,进而可得
,进而可得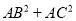
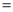 ;(用
;(用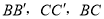 表示)
表示)
若AB=4,AC=3,BC=6,则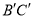
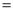 .
.
查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
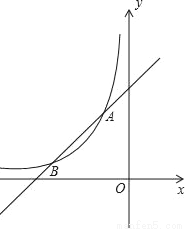
如图,函数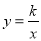 (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(1)求k,a,b的值;
(2)直线x=m与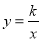 (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
查看答案和解析>>
科目: 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
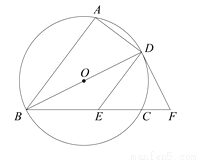
如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF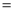 DE.
DE.
(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若 AD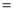 4,DE
4,DE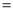 5,求DM的长.
5,求DM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com