
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
计算: 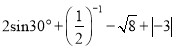 .
.
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
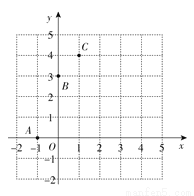
如图,函数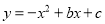 的图象经过点A,B,C.
的图象经过点A,B,C.
(1)求b,c的值;
(2)画出这个函数的图象.
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
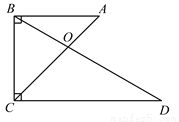
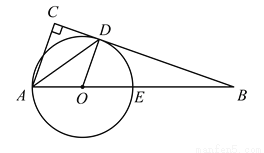
如图,∠ABC=∠BCD=90°,∠A=45°,∠D=30°,BC=1,AC,BD交于点O.求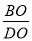 的值.
的值.
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
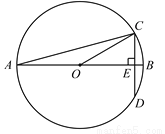
如图,AB是⊙O的直径,弦CD⊥AB于E,∠A=15°,AB=4.求弦CD的长.
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
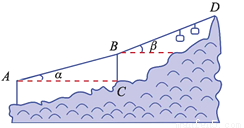
缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角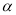 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
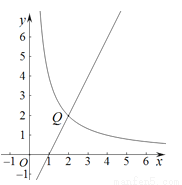
如图,在平面直角坐标系xOy中,函数y=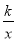 (k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(1)求m,k的值;
(2)已知点P(a,0)(a>0)是x轴上一动点,过点P作平行于y轴的直线,交直线y=2x﹣2于点M,交函数y=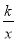 的图象于点N.
的图象于点N.
①当a=4时,求MN的长;
②若PM>PN,结合图象,直接写出a的取值范围.
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
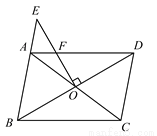
如图,在□ABCD中,对角线AC,BD交于点O,过点O作EO⊥BD,交BA延长线于点E,交AD于点F,若EF=OF,∠CBD=30°,BD=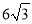 .求AF的长.
.求AF的长.
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
如图,点C是以AB为直径的⊙O上一动点,过点C作⊙O直径CD,过点B作BE⊥CD于点E.已知AB=6cm,设弦AC的长为xcm,B,E两点间的距离为ycm(当点C与点A或点B重合时,y的值为0).
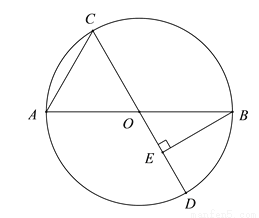
小冬根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小冬的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
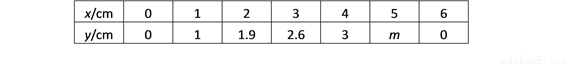
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)在(2)的条件下,当函数图象与直线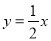 相交时(原点除外),∠BAC的度数是_____.
相交时(原点除外),∠BAC的度数是_____.
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O且经过A,D两点,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)AC=2,AB=6,求BE的长.
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
已知函数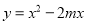 的顶点为点D.
的顶点为点D.
(1)求点D的坐标(用含m的代数式表示);
(2)求函数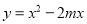 的图象与x轴的交点坐标;
的图象与x轴的交点坐标;
(3)若函数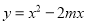 的图象在直线y=m的上方,求m的取值范围.
的图象在直线y=m的上方,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com