
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
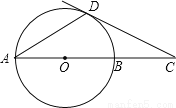
如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.求∠ADC的度数及AC的长.
查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
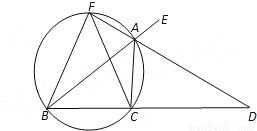
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FA•FD;
查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
(1) y=﹣2x2+120x﹣1600,20≤x≤40;(2) 30元/千克, 200元;(3)25. 【解析】 试题分析:(1)根据销售利润y=(每千克销售价﹣每千克成本价)×销售量w,即可列出y与x之间的函数关系式; (2)先利用配方法将(1)的函数关系式变形,再利用二次函数的性质即可求解; (3)先把y=150代入(1)的函数关系式中,解一元二次方程求出x,再根据x...查看答案和解析>>
科目: 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
(2016浙江省宁波市)从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=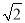 ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
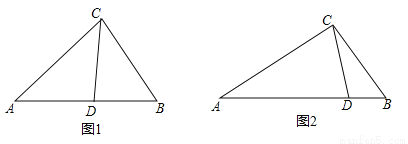
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:单选题
如图,AD∥BE∥CF,直线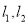 与这三条平行线分别交于点A,B,C和D,E,F.已知AB=1,BC=3,DE=2,则EF的长是( )
与这三条平行线分别交于点A,B,C和D,E,F.已知AB=1,BC=3,DE=2,则EF的长是( )
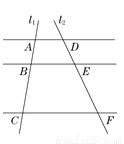
A. 4 B. 5 C. 6 D. 8
C 【解析】∵AD∥BE∥CF, ∴ , ∵AB=1,BC=3,DE=2, ∴ . 故选C.查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:单选题
下列各点在函数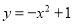 图象上的是( )
图象上的是( )
A. (0,0) B. (1,1) C. (0,﹣1) D. (1,0)
D 【解析】A. 把(0,0)代入得,左=0,右=1 ,故不符合题意; B. 把(1,1)代入得,左=1,右=-1+1=0 ,故不符合题意; C. 把(0,﹣1)代入得,左=-1,右=1 ,故不符合题意; D. 把(1,0)代入得,左=0,右=-1+0=0 ,故不符合题意; 故选D.查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:单选题
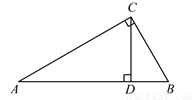
如图,Rt△ABC中,∠C=90°,∠A=30°,CD⊥AB于D,则△CBD与△ABC的周长比是( )
A. 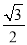 B.
B. 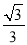 C.
C. 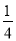 D.
D. 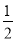
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:单选题
在Rt△ABC中,∠C=90°,AB=5,AC=3,则sinB的值是( )
A. 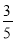 B.
B. 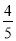 C.
C. 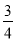 D.
D. 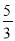
查看答案和解析>>
科目: 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:单选题
如图,△ABC内接于⊙O,连结OA,OB,∠ABO=40°,则∠C的度数是( )
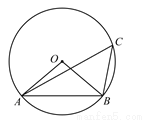
A. 100° B. 80° C. 50° D. 40°
C 【解析】∵OA=OB, ∴∠BAO=∠ABO=40°, ∴∠O=180°-40°-40°=100°, ∴ . 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com