时钟上的秒针旋转一周是60秒，则旋转10到秒时，形成的旋转角是（ ）度

A. 10 B. 20 C. 30 D. 60

D 【解析】试题解析：钟表的秒针匀速旋转一周需要60秒，即转过360度， 因而一秒转6度，则旋转10到秒时，形成的旋转角是6度， 故选D.

对于y=2(x-3)2+2的图象下列叙述正确的是( )

A. 顶点坐标为（-3，2） B. 当x≥3时，y随x增大而增大

C. 对称轴为y=3 D. 当x≥3时，y随x增大而减小

B 【解析】试题解析：∵y=2（x-3）2+2， ∴抛物线开口向上，对称轴为x=3，顶点坐标为（3，2）， ∴A、C不正确， ∵对称轴为x=3，开口向上， ∴当x≥3时，y随x的增大而增大， 故B正确，D不正确， 故选B．

二次函数y=x2的图象向右平移3个单位，得到新的图象的函数表达式是（　　）

A. y=x2+3 B. y=x2﹣3 C. y=（x+3）2 D. y=（x﹣3）2

D 【解析】原抛物线的顶点为（0，0），向右平移3个单位，那么新抛物线的顶点为（3，0）． 可设新抛物线的解析式为：y=（x﹣h）2+k， 代入得：y=（x﹣3）2， 故选D．

解方程:（2x+3）2=2x+3

【解析】试题分析：先移项，再运用因式分解法求解即可. 试题解析：移项， 添括号， 分解因式=0， 化简(2x+3)(2x+2)=0， 即2x+3=0或2x+2=0， ∴ .

（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；

（2）请画出△ABC绕点A顺时针方向旋转90度的⊿A″B″C″；

（3）写出B″的坐标，点B关于原点对称点B1的坐标.

（1）作图见解析；（2）作图见解析；（3）， . 【解析】（1）从三角形的各顶点向y轴引垂线并延长相同的长度，线段的端点就是要找的三顶点的对应点，顺次连接； （2）按要求作图即可； （3）根据平面直角坐标系写出点的坐标即可． 试题解析：（1）如图， （2）如图所示， （3）（-4，4），B1(3，-1)

观察下列计算

15× 15=1 ×2 ×100+25

25× 25=2×3 ×100+25

35× 35=3×4×100+25 ………

写出一般的规律为_________，请运用所学知识证明你的结论.

（10n+5)(10n+5)=100n(n+1)+25 【解析】试题分析：根据数字变化规律得出个位是5的两个相同的数的乘积等于这个数的十位数字乘以十位数字加1再乘以100再加25，进而得出答案． 试题解析：∵左边=25（2n-1）2=25（4n2-4n+1）=100n2-100n+25， 右边=100n2-100n+25， ∴左边=右边， ∴5（2n-1）×5（2n-...

已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．

（1）如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；

（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

（3）如果△ABC是等边三角形，试求这个一元二次方程的根．

【解析】 （1）△ABC是等腰三角形，理由见解析； （2）△ABC是直角三角形，理由见解析； （3）x1=0，x2=﹣1． 【解析】试题分析：（1）直接将x=-1代入得出关于a，b的等式，进而得出a=b，即可判断△ABC的形状； （2）利用根的判别式进而得出关于a，b，c的等式，进而判断△ABC的形状； （3）利用△ABC是等边三角形，则a=b=c，进而代入方程求出...

美化城市，改善人们的居住环境已成为城市建设的一项重要内容。某市城区近几年来，通过拆迁旧房、植草、栽树、修建公园等措施，使城区绿地面积不断增加(如图所示).

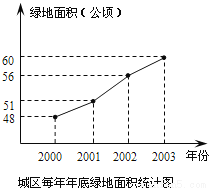
(1)根据图中所提供的信息，回答下列问题：2003年底绿地面积为 ____公顷，比2002年底增加了_____公顷；在2000年、2001年、2002年这三年中，绿地面积增加最多是_______年.

(2)为满足城市发展的需要，计划到2005年底使城区绿地总面积达到72．6公顷，试求2003年到2005年绿地面积的年平均增长率.

60 4 2002 【解析】试题分析：（1）仔细观察图象，根据图中数据一一作答即可； （2）根据图象和题中已知条件列出一元二次方程，解方程便可得出答案． 试题解析：（1）仔细观察图象可得： 2001年底的绿地面积为 60公顷， 比2000年底增加了4公顷； 在1999年，2000年，2001年这三年中，绿地面积增加最多的是2000年； （2）今明两年绿地面...

如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

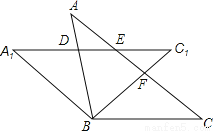
(1)求证：△BCF≌△BA1D.

(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。

(1)证明见解析(2)四边形A1BCE是菱形 【解析】试题分析：（1）根据等腰三角形的性质得到AB=BC，∠A=∠C，由旋转的性质得到A1B=AB=BC，∠A=∠A1=∠C，∠A1BD=∠CBC1，根据全等三角形的判定定理得到△BCF≌△BA1D；（2）由旋转的性质得到∠A1=∠A，根据平角的定义得到∠DEC=180°﹣α，根据四边形的内角和得到∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=...

现有一个产品销售点在经销某著名特色小吃时发现：如果每箱产品赢利10元，每天可销售50箱，若每箱产品涨价1元，日销量将减少2箱.

（1）现该销售点为使每天赢利600元，同时又要顾客得到实惠，那么每箱产品应涨价多少元？

（2）若该销售点单纯从经济角度考虑，每箱产品应涨价多少元?才能使每天的盈利最高？

（1）每箱应降价5元；（2）当时，才能使利润最大化. 【解析】试题分析：（1）设每箱应涨价x元，得出日销售量将减少2x箱，再由盈利额=每箱盈利×日销售量，依题意得方程求解即可； （2）设每箱应涨价x元，得出日销售量将减少2x箱，再由盈利额=每箱盈利×日销售量，依题意得函数关系式，进而求出最值． 试题解析：（1）设每箱应涨价x元. （10+x）（50-2x）=600 解...