甲、乙两人分别进行了5次射击训练，成绩如下（单位：环）．

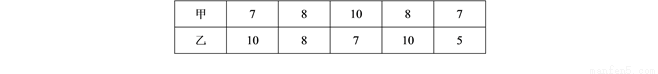
（1）甲射击成绩的中位数是 环，乙射击成绩的众数是 环；

（2）求甲射击成绩的方差．

（1）8环，10环 ；（2）1.2环2． 【解析】分析：（1）找出甲的中位数与乙的众数即可；（2）求出甲的方差即可. 本题解析： （1）对甲成绩进行排序：7,7,8,8,10. ∴中位数为8． 乙成绩出现次数最多的为10， ∴众数为10． (2) (分)， =1.2环.

一只不透明的袋子中装有1个蓝球和2个红球，这些球除颜色外都相同．

（1）搅匀后从中任意摸出1个球，求摸到蓝球的概率；

（2）搅匀后从中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1个球．

求至少有1次摸到红球的概率．

（1）；（2）． 【解析】分析：(1)列举出所有的可能结果,找到恰是蓝球的结果,根据概率公式计算即可, (2)列举出所有可能出现的结果,找到至少有一次是红球的结果,根据概率公式计算即可. 本题解析： (1)搅匀后从中任意摸出1个球,所有可能出现的结果有:红、红、蓝、共有3种,它们出现的可能性相同.所有的结果中,满足“恰好是蓝球”(记为事件A)的结果只有1种,所以;. ...

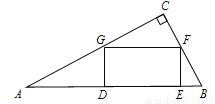
如图，在Rt△ABC中，∠C＝90°，矩形DEFG的顶点G、F分别在AC、BC上，DE在AB上．

（1）求证：△ADG∽△FEB；

（2）若AG＝5，AD＝4，求BE的长．

（1）证明见解析；（2）． 【解析】分析：（1）易证∠AGD=∠B，根据∠ADG=∠BEF=90°，即可证明△ADG∽△FEB；（2）根据勾股定理和相似三角形的性质解答即可. 本题解析： （1）∵∠C=90°，∴∠A+∠B=90°； ∵四边形DEFG是矩形，∴∠GDE=∠FED=90°，∴∠GDA=∠FED=90°； ∴∠A+∠AGD=90°，∴∠B=∠AGD且∠GD...

已知二次函数的图像经过点（0，3）、（3，0）和（1，4）．

（1）求该二次函数的表达式；

（2）若该二次函数图像的顶点为P，与x轴分别交于点A、B，求△ABP的面积．

（1）y=－x2+2x+3；（2）8． 【解析】分析：（1）设二次函数解析式y=ax2+ax+c,把三点坐标代入求出a,b,c的值，即可确定出二次函数解析式；（2）令y=0,求得点A,B的坐标，根据三角形的面积公式来求△ABP的面积. 本题解析：（1）设二次函数解析式y=ax2+ax+c，∵将点（0,3）、（3,0）和（1,4） 代入得 ，解得 ，∴y=－x2+2x+3； ...

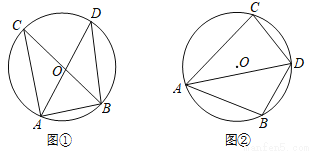
如图，已知⊙O的直径为10，点A、B、C在⊙O上，∠CAB的平分线交⊙O于点D．

（1）图①，当BC为⊙O的直径时，求BD的长；

（2）图②，当BD＝5时，求∠CDB的度数．

（1）；（2）120°． 【解析】分析;(1)连接CD，只要证明△ABD是等腰三角形是解题关键；（2）首先证明△OBD是等边三角形，推出∠BOD=60°,由,推出∠ACD=∠BAD=30°,推出∠BAC=60°,再利用圆内接四边形的性质即可解决问题. 本题解析： 解：（1）连接CD ∵∠CAB的平分线交⊙O于点D，∴∠CAD=∠DAB； ∴＝ ∴CD=DB ...

已知二次函数y＝x2＋（k－1）x－2k－3．

（1）求证：该二次函数图像与x轴总有两个公共点；

（2）若点A（－1，y1）、B（1，y2）在该二次函数的图像上，且y1＞y2，求k的取值范围．

（1）答案见解析；（2）k＜1． 【解析】分析：（1）根据△恒大于0即可证明；（2）将x=-1和x=1代入y＝x2＋（k－1）x－2k－3,再根据，可得结果. 本题解析： （1）由题意得，令，得到方程 a＝1，b＝k﹣1，c＝﹣2k﹣3，则b2﹣4ac＝（k﹣1）2﹣4（﹣2k﹣3）＝k2＋6k＋13＝（k＋3）2＋4，． ∵，∴（k＋3）2＋4＞0，即，∴方程有两个...

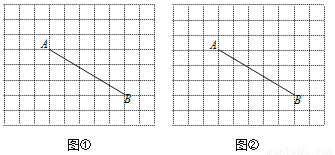
如图，边长为1的小正方形组成了网格，点A、B均是格点，请你仅用无刻度的直尺画出满足下列条件的点P，并在图中标出点P．

（1）图①中，点P在线段AB上且AP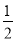＝AB；

（2）图②中，点P在线段AB上且AP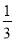＝AB．

答案见解析． 【解析】分析：（1）如图1，连接CD与AB的交点为P，由 ,可得AP=AB，则点P即为所求作点；（2）如图2，连接EF交AB于点Q，由 ,可得AP=AB，则点P即为所求作点． 本题解析：（1）AP=AB，即P为AB中点， 如图所示，矩形对角线交点即为所求． （2）AP=AB，即，运用相似三角形．

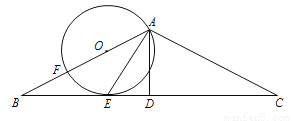
如图，在△ABC中，AB＝AC，AD为△ABC的中线，O为AB上一点，以O为圆心，AO为半径的⊙O与AB交于点F，与BC交于点E．连接AE，AE平分∠BAD．

（1）求证：BC与⊙O相切于点E；

（2）若AB＝10，BC＝16，求⊙O的半径；

（3）若AD与⊙O的交点为△ABC的重心，则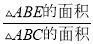的值为 ．

（1）答案见解析；（2）r=；（3）． 【解析】分析：（1）利用OA=OE得出∠AEO=∠OAE，再由角平分线得出∠BAE=∠DAE，即得出OE∥AD即可；（2）先求出CD=8，再用勾股定理求出AD=6，进而用角平分线定理即可得出BE=5，最后用相似三角形的性质得出结论；（3）先用切割线定理得出DE，进而用勾股定理得出AE，∠BAE=30°，即可得出BE=AE，即可得出结论． 本题解析...

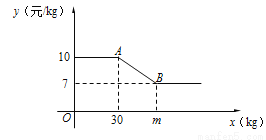
某水果店经营某种水果，顾客的批发量x（kg）与批发单价y（元/kg）之间的关系如图所示．图中线段AB表示：批发量x每增加1 kg，批发单价y降低0.1元/kg．

（1）求m的值；

（2）已知该水果进价为6元/kg，设该水果店获利w元．

①求w与x的函数表达式；

②当0＜x≤m时，求w的最大值．

（1）60；（2）当0＜x≤60时，w最大=122.5元． 【解析】分析:(1)利用价格变化规律，进而求出m的值；（2）①分类讨论：当0≤x＜30时，当30＜x≤60时，当x＞60时，分别得出等式；②当x满足条件0＜x≤60时，代入关系式，可求出总利润，比较后可得出最大利润． 本题解析： （1）m=（10-7）÷0.1+30=60． （2）①当0≤x＜30时，w1=（10-...

在矩形ABCD中，AB＝4，BC＝10，E是直线AD上任意一点（不与点A重合），点A关于直线BE的对称点为A′，AA′所在直线与直线BC交于点F．

（1）如图①，当点E在线段AD上时，①若△ABE ∽△DEC，求AE的长；

②设AE＝x，BF＝y，求y与x的函数表达式．

（2）线段DA′的取值范围是 ．

（1）①2或8；②y=；（2）≤DA′≤． 【解析】分析：（1）①设AE=x,再根据对应边成比例可得到关于x的一元二次方程，求解即可；②由，推出 ，由对应线段成比例得到关于x, y的方程，变形即可；（2）对称轴和对称点连线的交点在以线段AB为直径的圆上，D最短时 ， 在对角线BD. 本题解析： （）①设，则， ∵， ∴， 即， ∴， ∴， ， ...