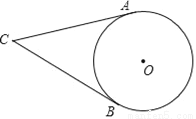
如图，CA，CB分别切⊙O于点A，B，D为圆上不与A，B重合的一点，已知∠ACB=58°，则∠ADB的度数为_____．

61°或119° 【解析】连接OA、OB， ∵CA、CB是⊙的切线，∴∠OAC=∠OBC=90°，∵∠ACB=58°，四边形OACB的内角和是360°，∴∠AOB=122°， 当点D在优弧ADB上时，∠AD1B=∠AOB=61°， 当点D在劣弧AB上时，根据圆内接四边形对角互补，可得∠AD2B=180°-∠AD1B=119°， 故答案为：61°或119°.

二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：下列结论：①ac＜0；②当x＞1时，y的值随x的增大而减小；③3是方程ax2+（b﹣1）x+c=0的一个根；④当﹣1＜x＜3时，ax2+（b﹣1）x+x＞0．其中正确的序号为_____

x	﹣1	0	1	3
y	﹣1	3	5	3

①③④ 【解析】利用待定系数法求出二次函数解析式为y=﹣x2+3x+3，可得ac=﹣1×3=﹣3＜0，故①正确； 对称轴为直线x=﹣， 所以，当x＞时，y的值随x值的增大而减小，故②错误； 方程为﹣x2+2x+3=0， 整理得，x2﹣2x﹣3=0， 解得x1=﹣1，x2=3， 所以，3是方程ax2+（b﹣1）x+c=0的一个根，正确，故③正确； ﹣1...

已知抛物线y=x2﹣2x﹣8与x轴的两个交点为A，B（A在左边），且它的顶点为P．

（1）求A、B两点的坐标

（2）求△PAB的面积．

（1）A（﹣2，0），B（4，0）；（2）27 【解析】试题分析：（1）令y=0，则有x2－2x－8＝0，解这个方程即可得A、B两点的横坐标，从而得到这两点的坐标； （2）求出抛物线顶点P坐标，再根据A、B的坐标，即可解决问题． 试题解析：（1）当y＝0时， x2－2x－8＝1， x１=4，x２=－2， ∴A（－2，0），Ｂ（4，0）， （2）y＝x2－2x－8...

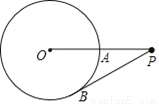
如图，P是⊙O外一点，OP交⊙O于A点，PB切⊙O于B点，已知OA=1，OP=2，求PB的长．

【解析】试题分析：连接OB，由切线的性质则可得∠B=90°，在Rt△POB在，利用勾股定理即可得. 试题解析：连接OB， ∵PB切⊙O于点B， ∴∠B=90°， ∵OA＝1， ∴OB＝OA＝R＝1， ∴OP＝2， ∴PB=.

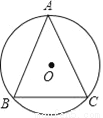
如图，△ABC内接于⊙O，∠A=45°，⊙O的半径为5，求BC的长．

5 【解析】试题分析：连接OB、OC，由圆周角定理则可得∠BOC=90°，然后利用勾股定理即可得. 试题解析：连接OB、OC. ∵∠A=45°，∴∠BOC=90°，∵OB=OC=R=5，∴BC= =5.

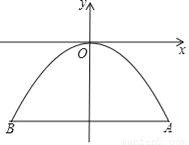
河上有一座桥孔为抛物线形的拱桥，水面宽为6米时，水面离桥孔顶部3米．把桥孔看成一个二次函数的图象，以桥孔的最高点为原点，过原点的水平线为横轴，过原点的铅垂线为纵轴，建立如图所示的平面直角坐标系．

（1）请求出这个二次函数的表达式；

（2）因降暴雨水位上升1米，此时水面宽为多少？

(1) 二次函数的表达式y=x2；（2）米 【解析】试题分析：（1）待定系数法求解可得； （2）求出y=﹣2时x的值，从而得出CD． 试题解析：（1）设抛物线解析式为y=ax2， 把x=3，y=﹣3代入，得a=， 这个二次函数的表达式y=x2； （2）把y=﹣2代入解y=x2得，x=， 所以CD=． 答：此时水面宽为米．

如图，A，P，B，C是半径为8的⊙O上的四点，且满足∠BAC=∠APC=60°，

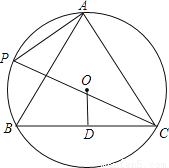
（1）求证：△ABC是等边三角形；

（2）求圆心O到BC的距离OD．

（1）证明见解析（2）4 【解析】【解析】 （1）证明：∵∠APC和∠ABC是同弧所对的圆周角，∴∠APC=∠ABC。 又∵在△ABC中，∠BAC=∠APC=60°，∴∠ABC=60°。 ∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°。 ∴△ABC是等边三角形。 （2）连接OB， ∵△ABC为等边三角形，⊙O为其外接圆， ∴O...

已知抛物线y=x2-(m+1)x+m，

（1）求证：抛物线与x轴一定有交点；

（2）若抛物线与x轴交于A(x1,0），B（x2,0）两点，x1﹤0﹤x2,且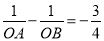,求m的值.

（1）证明见解析；（2）4. 【解析】试题分析：（1）先求出判别式，然后根据m为任意实数时，判别式的值是否大于等于0即可进行证明； （2）将所给的式子变形，然后利用根据与系数的关系可得=m+1， =m，代入即可得解. 试题解析：（1）∵∆=[-(m+1)]2-4m=(m-1)2，无论m为何值，都有(m-1)2≥0，即∆≥0， ∴抛物线与x轴一定有交点； （2）OA=-...

某商品的进价为每件20元，现在的售价为每件30元，每星期可卖出150件，市场调查反映：如果每件涨价1元（每件售价不能高于35元），那么每星期少卖10件，设每件涨价x元（x为非负整数），每星期销量为y件．

（1）求y关于x的函数解析式及自变量x的取值范围；

（2）如何定价才能使每星期的利润最大且每星期的销量较大？每星期的最大利润是多少？

（1）y=150﹣10x=﹣10x+150，（0≤x≤5且x为整数）；（2）当商品每件的售价为32时才能使每星期的利润最大且每星期的销量较大，每星期的最大利润是1560元 【解析】试题分析：（1）涨价为x元，可用x表示出每星期的销量，并得到x的取值范围； （2）根据总利润=销量×每件利润可得出利润的表达式，配方成顶点式即可得其最值情况． 试题解析：（1）设每件涨价x元，由题意得，...

如图①，AB为⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE=CB．

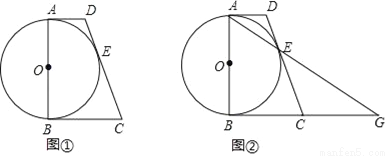
（1）求证：BC为⊙O的切线；

（2）连接AE并延长与BC的延长线交于点G（如图②所示）．若AB=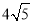，CD=9，求线段BC和EG的长．

（1）证明见解析（2） 【解析】试题分析：（1）连接OE，OC，即可证明△OEC≌△OEC，根据DE与⊙O相切于点E得到OEC=90°，从而证得∠OBC=90°，则BC是圆的切线． （2）先求线段BC的长，过D作DF⊥BG于F，则四边形ABFD是矩形，在Rt△DCF中，由切线长定理知AD=DE、CE=BC，利用勾股定理可求得CF的长，设AD=DE=BC，根据CD=9，列出方程即可求出x...