
��ͼ��A��P��B��C�ǰ뾶Ϊ8�ġ�O�ϵ��ĵ㣬�������BAC=��APC=60�㣬
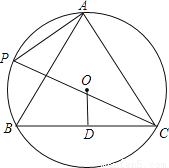
��1����֤����ABC�ǵȱ������Σ�
��2����Բ��O��BC�ľ���OD��
��1��֤����������2��4 ���������������� ��1��֤�����ߡ�APC�͡�ABC��ͬ�����Ե�Բ�ܽǣ����APC=��ABC�� �֡��ڡ�ABC�У���BAC=��APC=60�㣬���ABC=60�㡣 ���ACB=180�㩁��BAC����ABC=180�㩁60�㩁60��=60�㡣 ���ABC�ǵȱ������Ρ� ��2������OB�� �ߡ�ABCΪ�ȱ������Σ���OΪ�����Բ�� ��O... ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������������2017-2018ѧ�����꼶�ϲ���ѧ��ĩ�Ծ� ���ͣ������
ijУΪ���˽��һ�꼶
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
ijˮ�������̳�����һ�ָߵ�ˮ������ÿǧ��ӯ��10Ԫ��ÿ����۳�500ǧ�ˣ����г����鷢�֣��ڽ����۲��������£���ÿǧ���Ǽ�1Ԫ����������������20ǧ�ˣ��ָ��̳�Ҫ��֤ÿ��ӯ��6000Ԫ��ͬʱ��Ҫʹ�˿͵õ�ʵ�ݣ���
��1��ÿǧ��Ӧ�Ǽ۶���Ԫ��
��2����ˮ�������ۣ���ÿ��30�죩�Ƕ���ǧ�ˣ�
��1��ÿǧ��ˮ��Ӧ�Ǽ�5Ԫ����2����ˮ�������ۣ���ÿ��30�죩��12000ǧ�ˣ� �������������������1����ÿǧ��ˮ��Ӧ�Ǽ�Ԫ���ó���������������ǧ�ˣ�����ӯ����=ÿǧ��ӯ��������������������÷�����⼴�ɣ� ��2����������������30�����㼴�ɣ� ���������(1)��ÿǧ��ˮ��Ӧ�Ǽ�xԪ�� ������÷��̣�(500?20x)(10+x)=6000�� ����,�� ���������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
������x2��3x��4=0�������ֱ�Ϊx1��x2����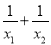 ��ֵ�ǣ� ��
��ֵ�ǣ� ��
A��1 B��2 C����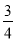 D����
D����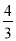
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
���б������ĸ�������һԪ���η��̣� ��
A. 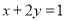 B.
B. 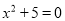 C.
C. 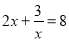 D.
D. 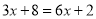
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡʮ���е�������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
���κ���y=ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ��������н��ۣ���ac��0���ڵ�x��1ʱ��y��ֵ��x���������С����3�Ƿ���ax2+��b��1��x+c=0��һ�������ܵ���1��x��3ʱ��ax2+��b��1��x+x��0��������ȷ�����Ϊ_____
x | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡʮ���е�������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��֪���κ���y��kx2��6x��9��ͼ����x�����������㣬��k��ȡֵ��ΧΪ�� ��
A. k>��1 B. k>��1��k��0 C. k�ݣ�1 D. k<��1��k��0
B ��������������ã���>0����k��0����(-6)2-4��k��(-9)>0����k��0������k>-1��k��0�� ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����а�����2017-2018ѧ����꼶��ѧ��������ѧ�Ծ����������� ���ͣ������
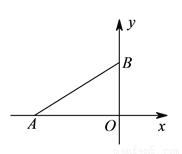
��ͼ����ƽ��ֱ������ϵ�У� 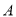 ��
�� 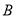 ���������ֱ�Ϊ
���������ֱ�Ϊ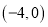 ��
�� 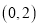 ������
������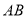 �����Ե�
�����Ե�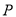 ��
�� 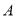 ��
�� 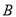 Ϊ������������ǵ���ֱ�������Σ����
Ϊ������������ǵ���ֱ�������Σ����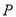 ����Ϊ__________��
����Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�γ���2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
һ�ž���ֽƬ������һ�������Σ�ʣ��һ�����Σ���Ϊ��һ�β�������ʣ�µľ���ֽƬ���ټ���һ�������Σ�ʣ��һ�����Σ���Ϊ�ڶ��β������������ڵ�n�β�����ʣ�µľ���Ϊ�����Σ����ԭ����Ϊn��������Σ�
��1����ͼ1������ABCD�У���AB=3��BC=9����ƾ���ABCDΪ������������Σ�
��2����ͼ2������ABCD��Ϊ7����Ϊ3�������������������ǣ���д�����Ǽ���������Σ�����ͼ�л����ü��ߣ�������ǣ���˵�����ɣ�
��3����֪����ABCD��һ�߳�Ϊ20����һ�߳�Ϊa��a��20����������3��������Σ��뻭������ABCD���ü��ߵ�ʾ��ͼ������ͼ���·�ֱ��д��a��ֵ��
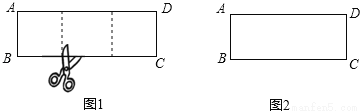
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com