
科目: 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
计算: 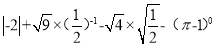 .
.
查看答案和解析>>
科目: 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
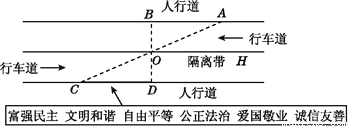
杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
查看答案和解析>>
科目: 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
已知关于x的一元二次方程mx2﹣(m+2)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
(1)证明见解析;(2)m=1. 【解析】试题分析:(1)求出方程根的判别式,利用配方法进行变形,根据平方的非负性证明即可; (2)利用一元二次方程求根公式求出方程的两个根,根据题意求出m的值. (1)证明:△=(m+2)2﹣8m =m2﹣4m+4 =(m﹣2)2, ∵不论m为何值时,(m﹣2)2≥0, ∴△≥0, ∴方程总有实数根; (2)【...查看答案和解析>>
科目: 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
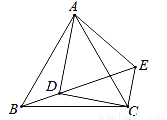
如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
查看答案和解析>>
科目: 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
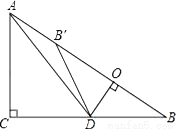
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目: 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
宜昌BRT快速公交系统及东山大道改造工程于2014年2月正式施工建设,成为宜昌近几年最大的市政工程和“一号民生工程”,全长约为23.8公里,是宜昌市现阶段客流量最为集中的干线客运走廊之一.
(1)如果一条行车道供小汽车使用,每小时最多能通过700辆车,且每辆小汽车平均乘座3人,但如果该车道专供BRT使用,每小时只能通过100辆公交车,但运送的总乘客数约是小汽车的7倍,求每辆公交平均乘座约多少人?(结果精确到十位)
(2)该工程包括前期设计、施工建设与投入试用三个阶段.已知试用期是前期设计时间的2倍,施工建设的时间比前期设计与投入试用时间的总和还多8个月,若每月可完成施工建设1.4公理,问该工程何时投入试用阶段?
(3)小明的爸爸在东山大道旁租一商铺经营,2013年总营业额是24万元,总支出包括两部分:一是交房租6万元,二是其他开支占总收入的25%.2014年因为受到大道改造工程的影响,总利润下降了许多,而2015年随着大道改造工程的完工,总利润预计又有回升.若2014年较上年度总利润下降的百分数刚好和2015年较上年度总利润增长的百分数相同,则小明的爸爸预计在2015年获得的总利润比2013年的总利润少3万元,求2014年小明爸爸获得的利润因大道改造而下降的百分数.
(1)150人;(2)2015年7月进入试用阶段;(3)50%. 【解析】试题分析:(1)设每辆公交车平均乘座x人.根据每小时只能通过100辆公交车,但运送的总乘客数约是小汽车的7倍列出方程并解答; (2)设前期设计的时间为y个月.则由“已知试用期是前期设计时间的2倍,施工建设的时间比前期设计与投入试用时间的总和还多8个月,全长约为23.8公里”列出方程并解答; (3)设2014...查看答案和解析>>
科目: 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
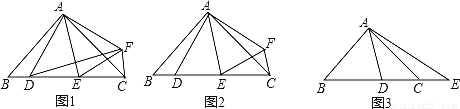
在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
下列方程一定是一元二次方程的是( )
A. 3x2+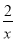 ﹣1=0 B. 5x2﹣6y﹣3=0 C. ax2﹣x+2=0 D. 3x2﹣2x﹣1=0
﹣1=0 B. 5x2﹣6y﹣3=0 C. ax2﹣x+2=0 D. 3x2﹣2x﹣1=0
查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
若关于x的方程x2+3x+a=0有一个根为-1,则另一个根为( )
A. -2 B. 2 C. 4 D. -3
A 【解析】试题分析:根据一元二次方程根与系数的关系,利用两根和,两根积,即可求出a的值和另一根. 设一元二次方程的另一根为x1,则根据一元二次方程根与系数的关系, 得﹣1+x1=﹣3, 解得:x1=﹣2.查看答案和解析>>
科目: 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
下列关于x的方程有实数根的是( )
A. x2﹣x+1=0 B. x2+x+1=0 C. x2﹣x﹣1=0 D. (x﹣1)2+1=0
C 【解析】A、△=b2﹣4ac=1﹣4=﹣3<0,此方程没有实数根; B、△=b2﹣4ac=1﹣4=﹣3<0,此方程没有实数根; C、△=b2﹣4ac=1+4=5>0,此方程有两个不相等的实数根; D、△=b2﹣4ac=4﹣8=﹣4<0,此方程没有实数根. 故选:C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com