
已知关于x的一元二次方程mx2﹣(m+2)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
(1)证明见解析;(2)m=1. 【解析】试题分析:(1)求出方程根的判别式,利用配方法进行变形,根据平方的非负性证明即可; (2)利用一元二次方程求根公式求出方程的两个根,根据题意求出m的值. (1)证明:△=(m+2)2﹣8m =m2﹣4m+4 =(m﹣2)2, ∵不论m为何值时,(m﹣2)2≥0, ∴△≥0, ∴方程总有实数根; (2)【...科目:初中数学 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
二次函数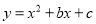 的图象经过点
的图象经过点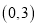 ,
, 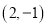 .
.
(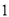 )求
)求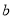 ,
, 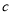 的值.
的值.
(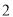 )求该二次函数图象的对称轴及与
)求该二次函数图象的对称轴及与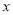 轴交点坐标.
轴交点坐标.
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
阅读材料:如图1,若点P是⊙O外的一点,线段PO交⊙O于点A,则PA长是点P与⊙O上各点之间的最短距离.
证明:延长PO交⊙O于点B,显然PB>PA.
如图2,在⊙O上任取一点C(与点A,B不重合),连结PC,OC.
∵PO<PC+OC,
且PO=PA+OA,OA=OC,
∴PA<PC
∴PA 长是点P与⊙O上各点之间的最短距离.
由此可以得到真命题:圆外一点与圆上各点之间的最短距离是这点到圆心的距离与半径的差.请用上述真命题解决下列问题.
(1)如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是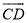 上的一个动点,连接AP,则AP长的最小值是 .
上的一个动点,连接AP,则AP长的最小值是 .
(2)如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,①求线段A’M的长度; ②求线段A′C长的最小值.
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
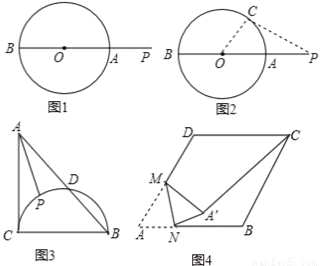
如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a=1,则b=( )
A. 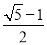 B.
B. 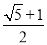 C.
C. 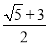 D.
D. 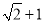
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
下列方程一定是一元二次方程的是( )
A. 3x2+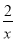 ﹣1=0 B. 5x2﹣6y﹣3=0 C. ax2﹣x+2=0 D. 3x2﹣2x﹣1=0
﹣1=0 B. 5x2﹣6y﹣3=0 C. ax2﹣x+2=0 D. 3x2﹣2x﹣1=0
查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:单选题
不等式组 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
A. 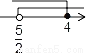 B.
B. 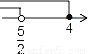 C.
C. 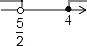 D.
D. 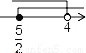
查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:单选题
把0.22×105改成科学记数法的形式,正确的是( )
A. 2.2×103 B. 2.2×104 C. 2.2×105 D. 2.2×106
B 【解析】试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,n的值为原数的整数位数减1,所以0.22×105=22000=2.2×104.故答案选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区观成中学2018届九年级上学期期中数学试卷 题型:填空题
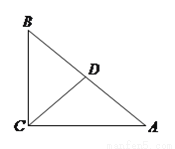
如图,已知在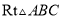 中,
中, 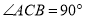 ,点
,点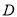 在
在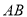 上,
上, 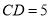 ,
, 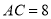 ,
, 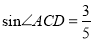 ,则
,则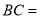 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
已知关于x的一元二次方程x2-2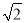 x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是x1,x2,求代数式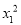 +
+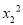 -
-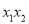 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com