
科目: 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:填空题
如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上的一动点,连结OP,将线段OP绕点D逆时针旋转60°得到线段OD,要使点D恰好落在BC上,求AP的长.
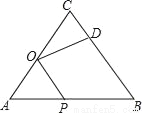
查看答案和解析>>
科目: 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:解答题
“六一”儿童节期间,某儿童用品商店设置了如下促销活动:如果购买该店100元以上的商品,就能参加一次游戏,即在现场抛掷一个正方体两次(这个正方体相对的两个面上分别画有相同图案),如果两次都出现相同的图案,即可获得价值20元的礼品一份,否则没有奖励.求游戏中获得礼品的概率是多少?
【解析】试题分析:依据题意先用列表法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率. 试题解析:设这三种图案分别用A、B、C表示,则列表得 第一次 第二次 A B C A (A,A) (A,B) (A,C) B (B,A) (B,B) (B,C) C (C,A) (C,B) (C...查看答案和解析>>
科目: 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:解答题
某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率.
(1)2.6(1+x)2 (2)可变成本平均每年增长的百分率为10% 【解析】试题分析: (1) 将基本等量关系“本年的可变成本=前一年的可变成本+本年可变成本的增长量”以及“本年可变成本的增长量=前一年的可变成本×可变成本平均每年增长的百分率”综合整理可得:本年的可变成本=前一年的可变成本×(1+可变成本平均每年增长的百分率). 根据这一新的等量关系可以由第1年的可变成本依次递推求出...查看答案和解析>>
科目: 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:解答题
如图,已知直线PA交⊙O于A、B两点,CD是⊙O的切线,切点且C,过点C作CD⊥PA于D,若AD:DC=1:3,AB=8,求⊙O的半径.
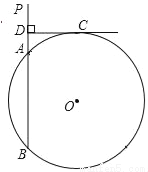
查看答案和解析>>
科目: 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:解答题
已知关于x的一元二次方程x2-mx-2=0.
(1)若-1是方程的一个根,求m的值和方程的另一个根.
(2)对于任意实数m,判断方程根的情况,并说明理由
(1)2(2)证明见解析 【解析】试题分析:(1)把x=﹣1代入原方程即可求出m的值,解方程进而求出方程的另一个根; (2)由一元二次方程的判别式计算的结果和0比较大小即可知道方程根的情况查看答案和解析>>
科目: 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:解答题
如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
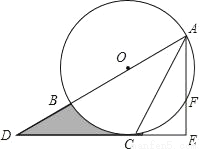
查看答案和解析>>
科目: 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:解答题
如图,在平面直角坐标系中,直线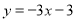 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线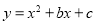 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
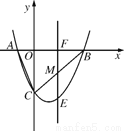
(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
见解析 【解析】 试题分析:(1)由求出点A,C的坐标,然后带入,解方程组即可;(2)求出直线BC的解析式是y=x-3,根据点M在直线BC 上,设M(x,x-3),则E(x,x2-2x-3) ,表示出线段ME的长,用配方法可求出最大值;(3)设在抛物线x轴下方存在点P,使以P,M,F,B为顶点的四边形是平行四边形,求出点P的坐标,然后判断点P是不是在抛物线上即可. 试题解析...查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第6章 反比例函数 单元测试卷 题型:单选题
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )
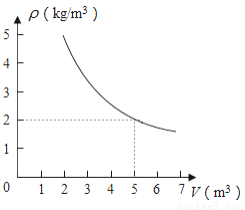
A. 5kg/m3 B. 2kg/m3 C. 100kg/m3 D. 1kg/m3
D 【解析】本题考查的是反比例函数的应用 先根据图象求出反比例函数关系式,即可求得当时,气体的密度。 设反比例函数关系式是, 图象过点(5,2) ,解得, 反比例函数关系式是, 当时,, 故选D。查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第6章 反比例函数 单元测试卷 题型:单选题
如图,直线y1=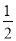 x+2与双曲线y2=
x+2与双曲线y2=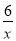 交于A(2,m),B(-6,n)两点.则当y1<y2时,x的取值范围是( )
交于A(2,m),B(-6,n)两点.则当y1<y2时,x的取值范围是( )
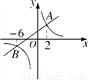
A. x>-6或0<x<2 B. -6<x<0或x>2 C. x<-6或0<x<2 D. -6<x<2
C 【解析】试题解析:观察函数图象,发现: 当x<-6或0<x<2时,直线y1=x+2的图象在双曲线y2=的图象的下方, ∴当y1<y2时,x的取值范围是x<-6或0<x<2. 故选C.查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第6章 反比例函数 单元测试卷 题型:单选题
如图,在同一直角坐标系中,函数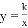 与
与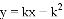 的大致图象是( )
的大致图象是( )
A. 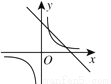 B.
B. 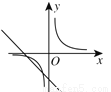 C.
C. 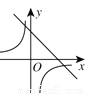 D.
D. 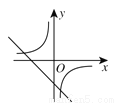
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com