相关习题
0 321374 321382 321388 321392 321398 321400 321404 321410 321412 321418 321424 321428 321430 321434 321440 321442 321448 321452 321454 321458 321460 321464 321466 321468 321469 321470 321472 321473 321474 321476 321478 321482 321484 321488 321490 321494 321500 321502 321508 321512 321514 321518 321524 321530 321532 321538 321542 321544 321550 321554 321560 321568 366461
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:单选题
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
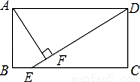
A. △AFD≌△DCE B. AF=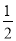 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
C
【解析】A.由矩形ABCD,AF⊥DE可得∠C=∠AFD=90°,AD∥BC,∴∠ADF=∠DEC.
又∵DE=AD,∴△AFD≌△DCE(AAS),故A正确;
B.∵∠ADF不一定等于30°,∴直角三角形ADF中,AF不一定等于AD的一半,故B错误;
C.由△AFD≌△DCE,可得AF=CD,由矩形ABCD,可得AB=CD,∴AB=AF,故C正确;
D.由△AF...
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:单选题
矩形具有而菱形不具有的性质是( )
A. 对角线相等 B. 两组对边分别平行
C. 对角线互相平分 D. 两组对角分别相等
A
【解析】【解析】
∵矩形具有的性质是:对角线相等且互相平分,两组对边分别平行,两组对角分别相等;菱形具有的性质是:两组对边分别平行,对角线互相平分,两组对角分别相等;
∴矩形具有而菱形不具有的性质是:对角线相等.
故选A.
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:填空题
如图,在矩形ABCD中,AB=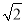 ,E是BC的中点,AE⊥BD于点F,则CF的长是_______.
,E是BC的中点,AE⊥BD于点F,则CF的长是_______.
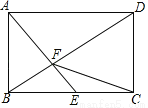
【解析】试题解析:∵四边形ABCD是矩形,
∵AE⊥BD,
∴△ABE∽△ADB,
∵E是BC的中点,
过F作FG⊥BC于G,
故答案为:
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:填空题
如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为__.
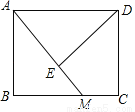
【解析】试题解析:∵四边形ABCD是矩形,
∴∠AMB=∠DAE,
∵DE=DC,
∴AB=DE,
∵DE⊥AM,
在△ABM和△DEA中,
∴AM=AD,
∵AE=2EM,
∴BC=AD=3EM,
连接DM,如图所示:
在和中,
∴EM=CM,
∴BC=3CM,
设EM=CM=x,则BM=2x,AM=BC=3x,
...
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:填空题
如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=________.
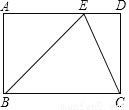
5
【解析】∵四边形ABCD是矩形,∴AD∥BC,AD=BC,AB=CD,∠D=90°.
∴∠AEB=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABE=∠AEB,∴AE=AB.
∴CD=AE=4,DE=AD-AE=BC-AE=7-4=3.
在Rt△CDE中,根据勾股定理得CE=.
故答案为5.
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:填空题
如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE= 4,AF=CE=3,则EF等于____.
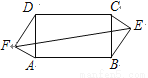
【解析】由题意得: 都是直角三角形.
,
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:填空题
如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,
则△AEF的面积为______.
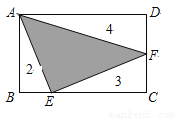
7
【解析】试题解析:设AB=a,BC=b,
∵△CEF,△ABE,△ADF的面积分别是2,3,4,
∴S△ABE=×a×BE=2,
∴BE=,
∴EC=BC-BE=b-,
∵S△CEF=×EC×FC=3,
∴FC=,
∴DF=CD-CF=a-,
∴S△ADF=×(a-)×b=4,
∴(ab)2-18ab+32=0,
解得:ab=1...
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:填空题
如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是_____.
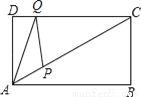
3
【解析】作点A关于直线CD的对称点E,作EP⊥AC于P,交CD于点Q.
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴DQ⊥AE,∵DE=AD,
∴QE=QA,
∴QA+QP=QE+QP=EP,
∴此时QA+QP最短(垂线段最短),
∵∠CAB=30°,
∴∠DAC=60°,
在RT△APE中,∵∠APE=90°,AE=2AD=6...
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:填空题
如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为______.
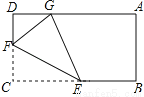
≤CF≤3
【解析】试题分析:∵四边形ABCD是矩形,
∴∠C=90°,BC=AD=5,CD=AB=3,
当点D与F重合时,CF最大=3,如图1所示:
当B与E重合时,CF最小,如图2所示:
在RTABG中,∵BG=BC=5,AB=3,
∴AG==4,
∴DG=AD﹣AG=1,设CF=FG=x,
在RT△DFG中,∵DF2+DG2=FG2,
∴...
查看答案和解析>>
科目:
来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习
题型:解答题
如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.
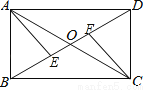
【解析】试题分析:(1)由矩形的性质得出OA=OC,OB=OD,AC=BD,∠ABC=90°,证出OE=OF,由SAS证明△AOE≌△COF,即可得出AE=CF;
(2)证出△AOB是等边三角形,得出OA=AB=6,AC=2OA=12,在Rt△ABC中,由勾股定理求出BC的长,即可得出矩形ABCD的面积.
试题解析:(1)证明:∵四边形ABCD是矩形,∴OA=OC,OB=OD,AC=B...
查看答案和解析>>


 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF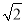 ,E是BC的中点,AE⊥BD于点F,则CF的长是_______.
,E是BC的中点,AE⊥BD于点F,则CF的长是_______.






