在扇形纸片AOB中，∠AOB=90°，OA=4，将扇形纸片AOB按如图所示折叠，使对折后点A与点O重合，折痕为DE，则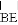的长度为__________．

【解析】试题分析：连接OE， ∵将扇形纸片AOB按如图所示折叠，使对折后点A与点O重合，折痕为DE， ∴OD＝OA＝OE，∠EDO＝90°， ∴∠DEO＝30°， ∴∠DOE＝60°， ∵∠AOB＝90°， ∴∠EOB＝30°， ∴弧BE的长度＝＝． 故答案为：．

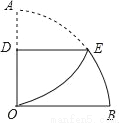
如图，在四边形ABCD中，∠BAD=∠C=90°，AB=AD，AE⊥CD，垂足为E，若线段AE=10，则S四边形ABCD=_____．

100 【解析】试题分析：过A作AF⊥BC，交CB的延长线于F， ∵AE⊥CD，∠C＝90° ∴∠AED＝∠F＝∠C＝90°，∴四边形AFCE是矩形， ∴∠FAE＝90°， ∵∠DAB＝90°， ∴∠DAE＝∠BAF＝90°﹣∠BAE， 在△AFB和△AED中， ， ∴△AFB≌△AED（AAS）， ∴AE＝AF＝10，S△AFB＝S△A...

解下列方程

（1）2x2﹣4x=12

（2）4x（2x+1）=6x+3．

(1)x=1±（2）x=﹣或x= 【解析】试题分析：（1）用配方法求【解析】 方程两边除以2把二次项系数化为1，然后两边加上一次项系数一半的平方，使左边化为完全平方式，右边是常数项，然后直接开平方求解即可； （2）把方程右边的项提出公因式3后移至左边，再利用提出公因式(2x＋1)，使方程转化为两个因式的积等于0的形式，然后转化为两个一元一次方程求解即可． 试题解析： 【解...

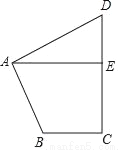
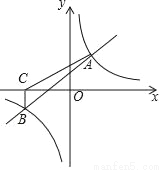
如图，一次函数y=x+2与反比例函数y=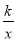的图象相交于A（2，m），B（﹣4，n）两点．

（1）求反比例函数的解析式；

（2）根据所给条件，请直接写出不等式x+2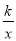＞的解集：　 　；

（3）过点B作BC⊥x轴，垂足为C，连接AC，求S△ABC．

（1）y=；（2）﹣4＜x＜0或x＞2；（3）6 【解析】试题分析：（1）把A点坐标代入一次函数解析式，求出m的值，然后把A点坐标代入反比例函数解析式求出k的值即可； （2）结合图象，使不等式成立的x值即是直线在双曲线上方时对应的自变量x的取值范围； （3）把B点坐标代入一次函数解析式，求出n的值，然后根据A点和B点坐标求出BC和BC边上的高，然后根据三角形的面积公式求解即可． ...

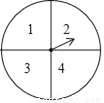
元旦期间，某商场设置了如图所示的幸运转盘，转盘分成4个大小相同的扇形，分别标有数学1，2，3，4，指针的位置固定，转盘可以自由转动，当转动的转盘停止后，其中的某个扇形会停在指针所指的位置（指针指向两个扇形的交线时，当作右边的扇形）．商场规定：凡是参加抽奖的顾客均可转动转盘两次，如果两次转动中指针指缶扇形上的数字之和为8是一等奖，数字之和为7是二等奖，数字之和为6是三等奖，标号之和为其他数字则获得一份纪念品，请分别求出顾客抽中一、二、三等奖的概率．

【解析】试题分析：画树状图展示所有16种等可能出现的结果数，再找出转出的两个数字之和为8的结果数、数字之和为7的结果数和数字之和为6的结果数，然后根据概率公式求解． 试题解析： 【解析】 画出树状图为： 由树状图可以看出，所有可能出现的结果共有16种，并且每种结果出现的可能性都相等．其中转出的两个数字之和为8的结果有1种，数字之和为7的结果有2种，数字之和为6的结果有3种， ...

近年来，随着百姓生活水平不断攀升，某市家庭轿车拥有量大幅增长，据统计，2013年该市家庭轿车拥有量为48万辆，2015年该市家庭轿车拥有量为69.12万辆．

（1）求2013年至2015年该市汽车拥有量的年平均增长率；

（2）由于我国汽车购置税减半优惠政策于2016年12月31日结束，因而2016年底该市迎来一轮购车热潮，据权威部门估计，2016年该市家庭轿车拥有量的年增长率比前两年的年平均增长率提高了10个百分点，求2016年该市家庭轿车的拥有量．

（1）20%；（2）截止2016年底该市家庭轿车的拥有量为89.856万辆． 【解析】试题分析：（1）设家庭轿车拥有量的年平均增长率为x，则增长2次以后的车辆数是48(1＋x)2，列出一元二次方程求解即可； （2）2016年的车辆＝2015年的车辆×(1＋x＋10%)． 试题解析： 【解析】 （1）设2013年底至2015年底该市汽车拥有量的年平均增长率为x， 根据...

阅读下列材料，完成相应学习任务：

四点共圆的条件

我们知道，过任意一个三角形的三个顶点能作一个圆，过任意一个四边形的四个顶点能作一个圆吗？小明经过实践探究发现：过对角互补的四边形的四个顶点能作一个圆，下面是小明运用反证法证明上述命题的过程：

已知：在四边形ABCD中，∠B+∠D=180°．

求证：过点A、B、C、D可作一个圆．

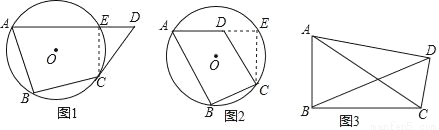
证明：如图（1），假设过点A、B、C、D四点不能作一个圆，过A、B、C三点作圆，若点D在圆外，设AD与圆相交于点E，连接CE，则∠B+∠AEC=180°，而已知∠B+∠D=180°，所以∠AEC=∠D，而∠AEC是△CED的外角，∠AEC＞∠D，出现矛盾，故假设不成立，因此点D在过A、B、C三点的圆上．

如图（2）假设过点A、B、C、D四点不能作一个圆，过A、B、C三点作圆，若点D在圆内，设AD的延长线与圆相交于点E，连接CE，则∠B+∠AEC=180°，而已知∠B+∠ADC=180°，所以∠AEC=∠ADC，而∠ADC是△CED的外角，∠ADC＞∠AEC，出现矛盾，故假设不成立，因此点D在过A、B、C三点的圆上．

因此得到四点共圆的条件：过对角互补的四边形的四个顶点能作一个圆．

学习任务：

（1）材料中划线部分结论的依据是　 　．

（2）证明过程中主要体现了下列哪种数学思想：　 　（填字母代号即可）

A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想

（3）如图（3），在四边形ABCD中，∠ABC=∠ADC=90°，∠CAD=16°．AD=BD，则求∠ADB的大小．

（1）圆的内接四边形对角互补（2）D；（3）∠ADB=32° 【解析】试题分析：（1）材料中划线部分结论的依据圆的内接四边形对角互补； （2）证明过程中分点D在圆外或圆内两种情形讨论，主要体现了分类讨论的数学思想； （3）利用“对角互补的四边形的四个顶点能作一个圆”这个结论，结合同弧所对的圆周角相等以及等腰三角形的性质，即可解决问题． 试题解析： 【解析】 （1）材...

为了响应国家“自主创业”的号召，某大学毕业生开办了一个装饰品商店，采购了一种今年刚上市的饰品进行了30天的试销，购进价格为20元/件，销售结束后，得知日销售量P（件）与销售时间x（天）之间的关系如图（1）所示，销售价格Q（元/件）与销售时间x（天）之间的关系如图（2）所示．

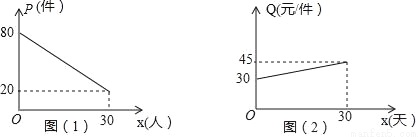
（1）根据图象直接写出：日销售量P（件）与销售时间x（天）之间的函数关系式为　 　；销售单价

Q（元/件）与销售时间x（天）的函数关系式为　 　．（不要求写出自变量的取值范围）

（2）写出该商品的日销售利润W（元）和销售时间x（天）之间的函数关系式；（不要求写出自变量的取值范围）

（3）请问在30天的试销售中，哪一天的日销售利润最大？并求出这个最大利润．

（1）P=﹣2x+80，Q=x+30；（2）W=﹣x2+20x+800；（3）在30天的试销中，第10天的日销售利润最大，最大利润为900元 【解析】试题分析：（1）设P＝kx＋80，将（30，20）代入可求出k的值，得出日销售量P（件）与销售时间x（天）之间的函数关系式；设Q＝mx＋30，将（30，45）代入可求出m的值，得出Q（元/件）与销售时间x（天）的函数关系式； （2）根据销...

综合与实践

问题情境

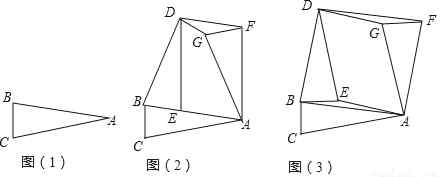
在综合实践课上，老师让同学们“以三角形的旋转”为主题进行数学活动，如图（1），在三角形纸片ABC中，AB=AC，∠B=∠C=α．

操作发现

（1）创新小组将图（1）中的△ABC以点B为旋转中心，逆时针旋转角度α，得到△DBE，再将△ABC以点A为旋转中心，顺时针旋转角度α，得到△AFG，连接DF，得到图（2），则四边形AFDE的形状是　 　．

（2）实践小组将图（1）中的△ABC以点B为旋转中心，逆时针逆转90°，得到△DBE，再将△ABC以点A为旋转中心，顺时针旋转90°，得到△AFG，连接DF、DG、AE，得到图（3），发现四边形AFDB为正方形，请你证明这个结论．

拓展探索

（3）请你在实践小组操作的基础上，再写出图（3）中的一个特殊四边形，并证明你的结论．

（1）平行四边形；（2）证明见解析（3）四边形AEDG是平行四边形． 【解析】试题分析：（1）由旋转的性质和旋转角度可求得DE∥AF，且DE＝AF，可证明四边形AFDE为平行四边形； （2）由旋转的性质和旋转角度可求得DE∥AF，且DE＝AF，可证明四边形AFDE为平行四边形，再由旋转角是90°，即可得出结论； （3）由旋转的性质和旋转角度判断出△ABE≌△DFG即可得出结论． ...

综合与探究

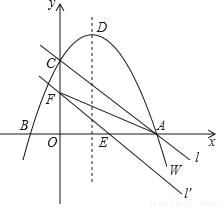
如图，在平面直角坐标系xOy中，抛物线W的函数表达式为y=﹣x2+2x+3，抛物线W与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，它的顶点为D，直线l经过A、C两点．

（1）求点A、B、C、D的坐标．

（2）将直线l向下平移m个单位，对应的直线为l′．

①若直线l′与x轴的正半轴交于点E，与y轴的正半轴交于点F，△AEF的面积为S，求S关于m的函数关系式，并写出自变量m的取值范围；

②求m的值为多少时，S的值最大？最大值为多少？

（3）若将抛物线W也向下平移m单位，再向右平移1个单位，使平移后得到的二次函数图象的顶点P落在△AOC的内部（不包括△AOC的边界），请直接写出m的取值范围．

（1）点D坐标为（1，4）（2）①S=﹣m2+m（0＜m＜3），②当m=时，S的值最大，最大值为（3）3＜m＜4 【解析】试题分析：（1）令y＝0，求出A，B的横坐标，令x＝0求出C的纵坐标，把二次函数解析式转化为顶点式即可得出D的坐标； （2）①利用待定系数法确定出直线l的解析式，根据平移得出l′的解析式，求出与坐标轴的交点E，F的坐标，得出AE，OF的长，最后用面积公式即可得出结论...