练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

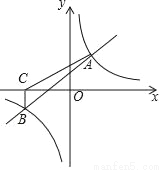
    如图，一次函数y=x+2与反比例函数y=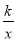的图象相交于A（2，m），B（﹣4，n）两点．

    （1）求反比例函数的解析式；

    （2）根据所给条件，请直接写出不等式x+2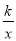＞的解集：　 　；

    （3）过点B作BC⊥x轴，垂足为C，连接AC，求S△ABC．

    （1）y=；（2）﹣4＜x＜0或x＞2；（3）6 【解析】试题分析：（1）把A点坐标代入一次函数解析式，求出m的值，然后把A点坐标代入反比例函数解析式求出k的值即可； （2）结合图象，使不等式成立的x值即是直线在双曲线上方时对应的自变量x的取值范围； （3）把B点坐标代入一次函数解析式，求出n的值，然后根据A点和B点坐标求出BC和BC边上的高，然后根据三角形的面积公式求解即可． ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：解答题

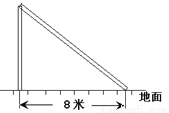
    如图，台风过后，一希望小学的旗杆在离地某处断裂，旗杆顶部落在离旗杆底部8米处，已知旗杆原长16米，请你求出旗杆在离底部多少米的位置断裂吗？

    旗杆在离底部6米处断裂 【解析】试题分析：旗杆折断的部分，未折断的部分和旗杆顶部离旗杆底部的部分构成了直角三角形，运用勾股定理可解决问题. 试题解析：设旗杆在离底部米的位置断裂，则折断部分的长为（16－x）米，根据勾股定理，得x2＋82＝（16－x）2， 解得x＝6， 即旗杆在离底部6米处断裂．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：解答题

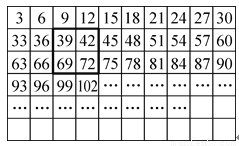
    若干个3的倍数按照一定的规律排成下表，用如图所示的正方形框出四个数．

    (1)如果框出的四个数的和是1158，你能确定四个数分别是多少吗？

    (2)你认为能否框出四个数，使这四个数的和是190.请说明理由．

    (1) 273，276，303，306.;(2) 不能 【解析】试题分析：（1）设四个数中最小的一个数是x，那么其余的三个数分别表示为x＋3、x＋30、x＋33，根据题意列方程，求解即可； （2）若设四个数中最小的为y，则有4y＋66＝190，解出y的值不是3的倍数，所以不在此数表中，因此不能框出四个数，使这四个数的和是190． 试题解析：【解析】 （1）设四个数中最小的一个数...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：单选题

    下列方程中，是一元一次方程的是（ ）

    A. x2-4x=3 B. 3x-1=， C. x+2y=1 D. xy-3=5

    B 【解析】A. 是一元二次方程，故此选项错误；B. 是一元一次方程，故此选项正确； C. 是二元一次方程，故此选项错误；D. 是二元二次方程，故此选项错误；故选：B.

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：解答题

    综合与实践

    问题情境

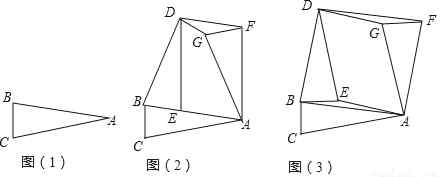
    在综合实践课上，老师让同学们“以三角形的旋转”为主题进行数学活动，如图（1），在三角形纸片ABC中，AB=AC，∠B=∠C=α．

    操作发现

    （1）创新小组将图（1）中的△ABC以点B为旋转中心，逆时针旋转角度α，得到△DBE，再将△ABC以点A为旋转中心，顺时针旋转角度α，得到△AFG，连接DF，得到图（2），则四边形AFDE的形状是　 　．

    （2）实践小组将图（1）中的△ABC以点B为旋转中心，逆时针逆转90°，得到△DBE，再将△ABC以点A为旋转中心，顺时针旋转90°，得到△AFG，连接DF、DG、AE，得到图（3），发现四边形AFDB为正方形，请你证明这个结论．

    拓展探索

    （3）请你在实践小组操作的基础上，再写出图（3）中的一个特殊四边形，并证明你的结论．

    （1）平行四边形；（2）证明见解析（3）四边形AEDG是平行四边形． 【解析】试题分析：（1）由旋转的性质和旋转角度可求得DE∥AF，且DE＝AF，可证明四边形AFDE为平行四边形； （2）由旋转的性质和旋转角度可求得DE∥AF，且DE＝AF，可证明四边形AFDE为平行四边形，再由旋转角是90°，即可得出结论； （3）由旋转的性质和旋转角度判断出△ABE≌△DFG即可得出结论． ...

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：填空题

    某农科所在相同条件下做某作物种子发芽率的试验，结果如下所示：

    种子个数

    100

    200

    300

    400

    500

    600

    700

    800

    900

    1000

    发芽种子个数

    94

    187

    282

    338

    435

    530

    624

    718

    814

    901

    发芽种子频率

    0.940

    0.935

    0.940

    0.845

    0.870

    0.883

    0.891

    0.898

    0.904

    0.901

    一般地，1000kg种子中大约有_____kg种子是不能发芽的．

    100 【解析】试题分析：∵大量重复试验发芽率逐渐稳定在0.9左右， ∴1000kg种子中不能发芽的种子的质量是： 1000×（1－0.9） ＝1000×0.1 ＝100（kg） 故答案为：100．

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：单选题

    已知关于x的方程x2+2x=m有两个相等的实数根，则m的值是（　　）

    A. 1 B. ﹣1 C. 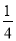D. ﹣

    B 【解析】试题分析：原方程可变形为x2＋2x－m＝0． ∵关于x的方程x2＋2x－m＝0有两个相等的实数根， ∴△＝22＋4m＝4＋4m＝0， 解得：m＝－1． 故选B．

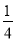
    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县九年级（上）期末数学试卷（五四学制） 题型：填空题

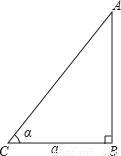
    如图所示，在建筑物AB的底部a米远的C处，测得建筑物的顶端A点的仰角为α，则建筑物AB的高可表示为_____．

    atanα 【解析】试题解析：∵在直角△ABC中，∠B=90°，∠C=α，BC=a， ∴tan∠C=， ∴AB=BC•tan∠C=a•tanα． 故答案为atanα．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：解答题

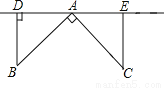
    如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.

    证明见解析. 【解析】试题分析：根据已知条件及互余关系可证△ABD≌△CAE，则BD=AE，AD=CE，由DE=AD+AE，得出线段DE=BD+CE． 试题解析：证明：∵∠BAC=90°，BD⊥DE，CE⊥DE， ∴∠DAB+∠DBA=∠DAB+∠EAC， ∴∠DBA=∠EAC； 在△ABD与△CAE中， ， ∴△ABD≌△CAE（AAS）， ∴BD...

    查看答案和解析>>

    同步练习册答案