相关习题
0 321522 321530 321536 321540 321546 321548 321552 321558 321560 321566 321572 321576 321578 321582 321588 321590 321596 321600 321602 321606 321608 321612 321614 321616 321617 321618 321620 321621 321622 321624 321626 321630 321632 321636 321638 321642 321648 321650 321656 321660 321662 321666 321672 321678 321680 321686 321690 321692 321698 321702 321708 321716 366461
科目:
来源:2018人教版八年级数学下册练习:第十八章达标检测卷
题型:填空题
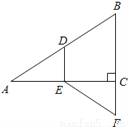
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=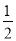 BC.若AB=12,求EF的长.
BC.若AB=12,求EF的长.
6
【解析】试题分析:如图,连接DC,根据三角形中位线定理可得,DE=BC,DE∥BC,又因CF=BC,可得DE=CF,根据一组对边平行且相等的四边形是平行四边形可得四边形CDEF是平行四边形,由平行四边形的性质可得EF=DC.在Rt△ABC中,根据直角三角形斜边的中线等于斜边的一半可得DC=AB=5,所以EF=DC=5.
查看答案和解析>>
科目:
来源:2018人教版八年级数学下册练习:第十八章达标检测卷
题型:填空题
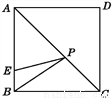
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是__________.
10
【解析】试题分析:根据题意得:AE=6,AD=AB=8,根据正方形的性质可得点B关于AC的对称轴为点D,连接DE,DE与AC的交点就是点P,则DE==10.
查看答案和解析>>
科目:
来源:2018人教版八年级数学下册练习:第十八章达标检测卷
题型:解答题
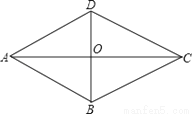
如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.
6
【解析】试题分析:根据菱形的性质得出AC⊥BD,DO=BO,然后根据Rt△AOB的勾股定理求出BO的长度,然后根据BD=2BO求出答案.
试题解析:∵四边形ABCD是菱形,对角线AC与BD相交于O, ∴AC⊥BD,DO=BO,
∵AB=5,AO=4, ∴BO==3, ∴BD=2BO=2×3=6
查看答案和解析>>
科目:
来源:2018人教版八年级数学下册练习:第十八章达标检测卷
题型:解答题
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
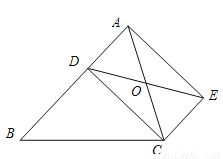
详见解析.
【解析】试题分析:根据CE∥AB,可得∠DAO=∠ECO,再由OA=OC,利用ASA可证明△ADO≌△ECO,根据全等三角形的性质可得AD=CE,再根据一组对边平行且相等的四边形是平行四边形即可判定四边形ADCE是平行四边形,由此可得出结论.
试题解析:【解析】
猜想线段CD与线段AE的大小关系和位置关系是:相等且平行.
理由:∵CE∥AB,
∴∠DAO=∠E...
查看答案和解析>>
科目:
来源:2018人教版八年级数学下册练习:第十八章达标检测卷
题型:解答题
如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D。
(1)求证:BE=CF ;
(2)当四边形ACDE为菱形时,求BD的长。
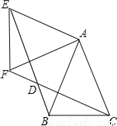
(1)证明见解析(2)-1
【解析】试题分析:(1)先由旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CD;
(2)由菱形的性质得到DE=AE=AC=AB=1,AC∥DE,根据等腰三角形的...
查看答案和解析>>
科目:
来源:2018人教版八年级数学下册练习:第十八章达标检测卷
题型:解答题
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

(1)证明见解析;(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形,理由见解析.
【解析】试题分析:(1)求出∠BAD=∠DAC,∠MAE=∠CAE,求出∠DAE的度数,求出∠AEC=∠ADC=∠EAD=90°,根据矩形的判定判断即可;
(2)求出AD=DC,得出∠ACD=∠DAC=45°,求出∠BAC=90°,即可求出答案.
试题解析:(1)证明:∵在△ABC...
查看答案和解析>>
科目:
来源:2018人教版八年级数学下册练习:第十八章达标检测卷
题型:解答题
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
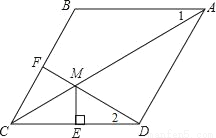
(1)2;(2)见解析.
【解析】试题分析:(1)根据菱形的对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠1=∠ACD,所以∠ACD=∠2,根据等角对等边的性质可得CM=DM,再根据等腰三角形三线合一的性质可得CE=DE,然后求出CD的长度,即为菱形的边长BC的长度;
(2)先利用“边角边”证明△CEM和△CFM全等,根据全等三角形对应边相等可得ME=MF,延长AB交DF于点G...
查看答案和解析>>
科目:
来源:2018人教版八年级数学下册练习:第十八章达标检测卷
题型:解答题
如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
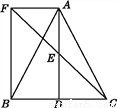
(1)证明见解析;(2)当AB=AC时,四边形AFBD是矩形,证明见解析.
【解析】试题分析:(1)根据平行线的性质得到∠AFE=∠DCE,由中点的定义得到AE=DE,根据三角形全等的判定易证得△AFE≌△DCE,利用全等三角形的性质得AF=DC,而AF=BD,即可得到D是BC的中点;
(2)在(1)的基础上,根据全等三角形的性质和有三个角都是直角的四边形是矩形.
试题解析:证明...
查看答案和解析>>
科目:
来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷
题型:单选题
查看答案和解析>>
科目:
来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷
题型:单选题
下列图形中,既是轴对称图形又是中心对称图形的是( )
A. 平行四边形 B. 菱形 C. 等边三角形 D. 等腰直角三角形
B
【解析】试题解析:A. 不是轴对称图形,是中心对称图形,故此选项错误,不合题意;
B. 是轴对称图形,也是中心对称图形,故此选项正确,符合题意;
C. 是轴对称图形,不是中心对称图形,故此选项错误,不合题意;
D. 无法确定是轴对称图形,也不是中心对称图形,故此选项错误,不合题意.
故选B.
查看答案和解析>>

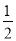 BC.若AB=12,求EF的长.
BC.若AB=12,求EF的长.







 的解为( )
的解为( ) B.
B.  C.
C.  ,
, 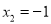 D.
D.  ,
, 