
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:填空题
若∠A是锐角,且sinA是方程2x2-x=0的一个根,则sinA=________.
【解析】通过题意,可先解方程2x2-x=0,得x=0或x=.然后由∠A是锐角,可知0<sin A<1,从而求得sinA=. 故答案为: .查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:填空题
如图所示,在等腰三角形ABC中,tan A= ,AB=BC=8,则AB边上的高CD的长是__.
,AB=BC=8,则AB边上的高CD的长是__.

查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:填空题
如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC对称,若DM=1,则tan∠ADN=________.
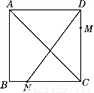
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:填空题
在Rt△ABC中,∠C=90°,且sin 30°= ,sin 45°=
,sin 45°= ,sin 60°=
,sin 60°= ,cos 30°=
,cos 30°=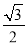 ,cos 45°=
,cos 45°=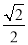 ,cos 60°=
,cos 60°=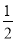 ;观察上述等式,当∠A与∠B互余时,请写出∠A的正弦函数值与∠B的余弦函数值之间的关系:______________.
;观察上述等式,当∠A与∠B互余时,请写出∠A的正弦函数值与∠B的余弦函数值之间的关系:______________.
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
计算:(1)2sin 30°+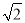 cos 45°-
cos 45°-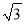 tan 60°;(2)tan230°+cos230°-sin245°tan 45°.
tan 60°;(2)tan230°+cos230°-sin245°tan 45°.
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
在Rt△ABC中,∠C=90°,BC=6,∠B=60°,解这个直角三角形.
∠A=30°,AB=12,AC=6. 【解析】试题分析:根据直角三角形的边角关系,合理变形,解直角三角形即可. 试题解析:因为∠B=60°,所以∠A=90°-∠B=90°-60°=30°. 因为sin A=,所以=,得AB=12. 因为tan B=,所以=,得AC=6.查看答案和解析>>
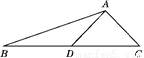
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
如图,AD是△ABC的中线,tan B=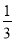 ,cos C=
,cos C=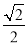 ,AC=
,AC=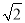 .求:
.求:
(1)BC的长;
(2)sin ∠ADC的值.
查看答案和解析>>
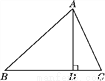
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sin C=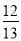 ,BC=12,求△ABC的面积.
,BC=12,求△ABC的面积.
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
如图,在四边形ABCD中,∠B=∠D=90°,AB=BC,AD=7,tan A=2.求CD的长.

查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
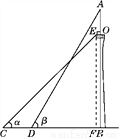
如图,某塔观光层的最外沿点E为蹦极项目的起跳点,已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据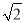 ≈1.4,
≈1.4, 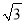 ≈1.7)
≈1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com