
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
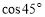 的值等于( )
的值等于( )
(A)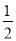 (B)
(B)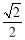 (C)
(C)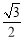 (D)
(D)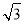
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
在Rt△ABC中,∠C=90°,AB=10,AC=6,则cos A的值是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
如图,要测量河两岸A,C两点间的距离,已知AC⊥AB,测得AB=a,∠ABC=α,那么AC等于( )
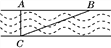
A. a·sin α B. a·cos α C. a·tan α D. 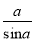
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则下列式子一定成立的是( )
A. a=c·sin B B. a=c·cos B C. b=c·sin A D. b=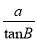
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
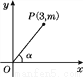
如图,在平面直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是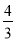 ,则sinα的值是( )
,则sinα的值是( )
A. 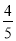 B.
B. 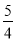 C.
C. 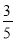 D.
D. 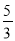
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
如图所示,在△ABC中, cos B=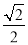 ,sin C=
,sin C=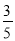 ,BC=7,则△ABC的面积是( )
,BC=7,则△ABC的面积是( )
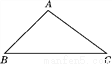
A. 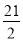 B. 12 C. 14 D. 21
B. 12 C. 14 D. 21
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
如图,在菱形ABCD中,DE⊥AB,cos A=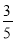 ,BE=2,则tan ∠DBE的值是( )
,BE=2,则tan ∠DBE的值是( )
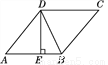
A. 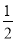 B. 2 C.
B. 2 C. 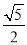 D.
D. 
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=2,则DE+DF=( )
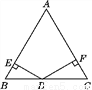
A. 1 B. 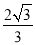 C.
C. 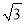 D.
D. 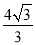
查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
阅读材料:因为cos 0°=1,cos 30°= ,cos 45°=
,cos 45°= ,cos 60°=
,cos 60°= ,cos 90°=0,所以,当0°<α<90°时,cosα随α的增大而减小.解决问题:已知∠A为锐角,且cos A<
,cos 90°=0,所以,当0°<α<90°时,cosα随α的增大而减小.解决问题:已知∠A为锐角,且cos A< ,那么∠A的取值范围是( )
,那么∠A的取值范围是( )
A. 0°<∠A<30° B. 30°<∠A<60° C. 60°<∠A<90° D. 30°<∠A<90°
C 【解析】根据余弦值的阅读材料,可由0<cosA<,得cos90°<cosA<cos60°,故60°<∠A<90°. 故选:C.查看答案和解析>>
科目: 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
如图,小叶与小高欲测量公园内某棵树DE的高度.他们在这棵树正前方的一座楼亭前的台阶上的点A处测得这棵树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得这棵树顶端D的仰角为60°.已知点A的高度AB为3 m,台阶AC的坡度为1∶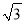 ,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
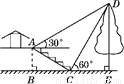
A. 6 m B. 7 m C. 8 m D. 9 m
D 【解析】过点A作AF⊥DE于点F,则四边形ABEF为矩形, ∴AF=BE,EF=AB=3m. 设DE=xm,在Rt△CDE中,CE==xm. 在Rt△ABC中,∵=,AB=3m, ∴BC=3m. 在Rt△AFD中,DF=DE-EF=(x-3) m, ∴AF== (x-3) m. ∵AF=BE=BC+CE, ∴ (x-3)=3+x, 解...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com