
科目: 来源:广东省汕头市澄海区2017-2018学年八年级上学期期末质量检测数学试卷 题型:解答题
观察下列等式的规律,解答下列问题:
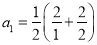 ,
, 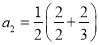 ,
, 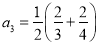 ,
, 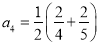 ,…….
,…….
(1)第5个等式为 ;第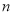 个等式为 (用含n的代数式表示,n为正整数);
个等式为 (用含n的代数式表示,n为正整数);
(2)设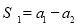 ,
, 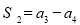 ,
, 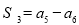 ,……,
,……, 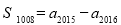 .
.
求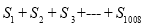 的值.
的值.
查看答案和解析>>
科目: 来源:广东省汕头市澄海区2017-2018学年八年级上学期期末质量检测数学试卷 题型:解答题
阅读下列材料,然后解决问题:
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
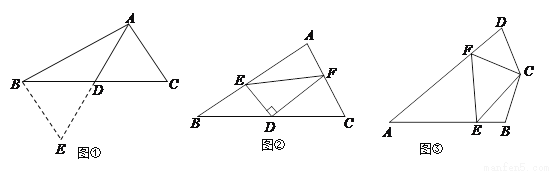
(1)如图①,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:单选题
方程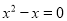 的解是( )
的解是( )
A. 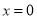 B.
B. 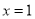 C.
C. 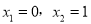 D.
D. 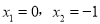
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:单选题
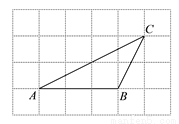
如图,在由边长为1的小正方形组成的网格中,点A、B、C都在小正方形的顶点上,则
tan∠CAB的值为
A. 1 B. 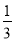 C.
C. 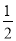 D.
D. 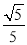
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:单选题
如图,在△ABC中,D为AB中点,DE∥BC交AC于E点,则△ADE与△ABC的面积比为( )
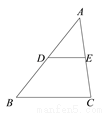
A. 1:1 B. 1:2 C. 1:3 D. 1:4
D 【解析】试题分析:∵DE∥BC, ∴△ADE∽△ABC, ∵D是边AB的中点, ∴AD:AB=1:2, ∴. 故选D.查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.右图是一段弯形管道,其中∠O=∠O'=90°,中心线的两条弧的半径都是1000mm,这整段变形管道的展直长度约为(π取3.14)( )
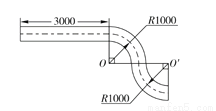
A. 6140mm B. 6280mm C. 9280mm D. 457mm
A 【解析】图中管道的展直长度=2×+3000=1000π+3000≈1000×3.14+3000=6140mm. 故选A.查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:单选题
(2016河北省)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
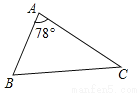
A. 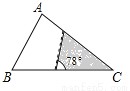 B.
B. 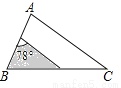
C. 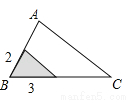 D.
D. 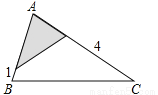
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:单选题
甲、乙、丙三名射箭运动员在某次测试中各射箭8次,三人的测试成绩如下表:
s2甲、s 2乙、s 2丙分别表示三名运动员这次测试成绩的方差,下面各式中正确的是( )

A. s 2甲>s 2乙>s 2丙 B. s 2丙>s 2乙>s 2甲
C. s 2丙>s 2甲>s 2乙 D. s 2乙>s 2甲>s 2丙
B 【解析】∵=(7×1+8×3+9×3+10×1) ÷8=8.5, 则s2甲=[(7-8.5)2+3×(8-8.5)2+3×(9-8.5)2+(10-8.5)2] ÷8=0.75; ∵=(7×2+8×2+9×2+10×2)÷8=8.5, ∴s2乙=[2×(7-8.5)2+2×(8-8.5)2+2×(9-8.5)2+2×(10-8.5)2] ÷8=1.25 ∵=(7×...查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:单选题
如图,点A,B,C,D,E为⊙O的五等分点,动点M从圆心O出发,沿线段OA→劣弧AC→线段CO的路线做匀速运动,设运动的时间为t,∠DME的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
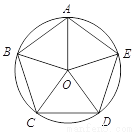
A. 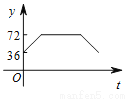
B. 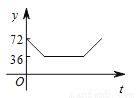
C. 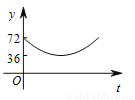
D. 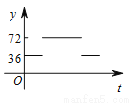
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com