
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:填空题
等腰三角形的一个外角等于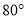 ,则它的顶角是__________.
,则它的顶角是__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:填空题
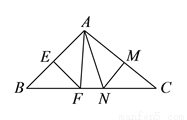
如图, 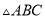 中,
中, 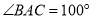 ,
, 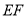 ,
, 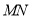 分别为
分别为 ,
,  的垂直平分线,如果
的垂直平分线,如果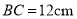 ,那么
,那么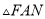 的周长为__________
的周长为__________ 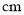 ,
, 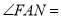 __________
__________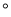 .
.
查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:填空题
已知等腰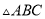 中,
中, 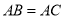 ,
, 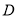 是
是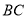 边上一点,连结
边上一点,连结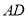 .若
.若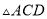 和
和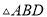 都是等腰三角形,则
都是等腰三角形,则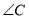 的度数为__________.
的度数为__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:填空题
如图,在 中,
中,  ,
,  ,点
,点 是
是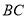 上的动点,过点
上的动点,过点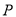 作
作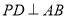 于点
于点 ,
, 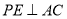 于点
于点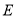 ,则
,则 __________.
__________.

查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:填空题
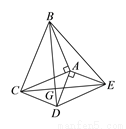
如图, 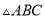 和
和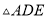 都是等腰直角三角形,
都是等腰直角三角形, 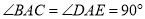 ,连接
,连接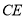 交
交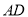 与
与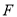 ,连接
,连接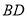 交
交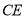 于点
于点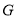 ,连接
,连接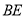 ,下列结论:①
,下列结论:①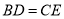 ;②
;②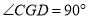 ;③
;③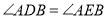 ;④
;④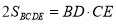 ;⑤
;⑤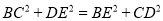 .正确的有__________.
.正确的有__________.
查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:解答题
解不等式:
( )
)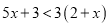 .
.
( )
)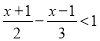 .
.
查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:解答题
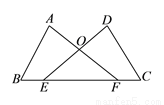
如图,点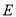 、
、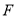 在线段
在线段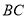 上,
上, 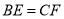 ,
, 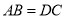 ,
,  ,
, 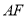 与
与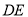 交于点
交于点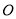 .求证:
.求证:
( )
)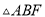 ≌
≌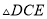 .
.
(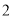 )试判断
)试判断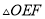 的形状.
的形状.
查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:解答题
如图,在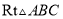 中,
中, 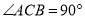 .
.
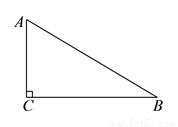
(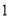 )用尺规在边
)用尺规在边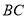 上求作一点
上求作一点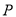 ,使
,使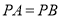 (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(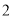 )连结
)连结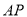 ,若
,若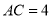 ,
, 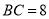 时,试求线段
时,试求线段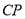 的长度.
的长度.
查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:解答题
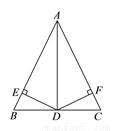
如图,在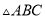 中,
中, 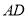 平分
平分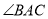 ,且
,且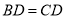 ,
, 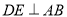 于点
于点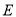 ,
, 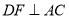 于点
于点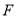 .
.
( )求证:
)求证: 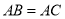 .
.
(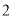 )若
)若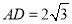 ,
, 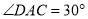 ,求
,求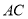 的长.
的长.
查看答案和解析>>
科目: 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:解答题
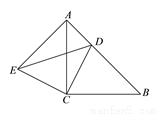
如图, 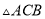 和
和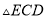 都是等腰直角三角形,
都是等腰直角三角形, 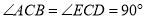 ,
,  为
为 边上一点.
边上一点.
求证:( )
)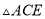 ≌
≌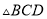 .
.
(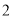 )
)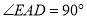 .
.
(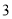 )
)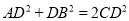 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com