
科目: 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:解答题
如图,已知抛物线y=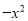 +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
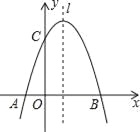
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目: 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:解答题
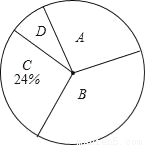
某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
查看答案和解析>>
科目: 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:解答题
A.B、C三把外观一样的电子钥匙对应打开a、b、c三把电子锁.
(1)任意取出一把钥匙,恰好可以打开a锁的概率是 ;
(2)求随机取出A、B、C三把钥匙,一次性对应打开a、b、c三把电子锁的概率.
(1) ;(2). 【解析】试题分析:(1)直接利用概率公式求解即可; (2)根据题意列表后利用概率公式求概率即可. 试题解析:(1)∵3把钥匙中有1把打开a锁, ∴任意取出一把钥匙,恰好可以打开a锁的概率是 故答案为: (2)由题意可列表如下: aA bB cC aA bC cB bA aB cC bA ...查看答案和解析>>
科目: 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:解答题
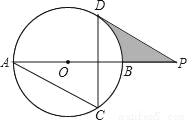
如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:解答题
2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
(1)y=-10x+300(12≤x≤30)(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为16元(3)当售价定为20元时,王大伯获得利润最大,最大利润是1000元. 【解析】试题分析:(1)设蝙蝠型风筝售价为x元时,销售量为y个,根据“当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个”,即可得出y关于x的函数关系式; (2)设王大伯获得的利...查看答案和解析>>
科目: 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:解答题
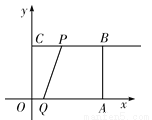
已知:如图所示,在平面直角坐标系xOy中,四边形OABC是矩形,OA=4,OC=3,动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动,设点P、点Q的运动时间为t(s).
(1)当t=1 s时,求经过点O,P,A三点的抛物线的解析式;
(2)当线段PQ与线段AB相交于点M,且BM=2AM时,求t(s)的值;
(3)连接CQ,当点P,Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.
查看答案和解析>>
科目: 来源:江苏省沭阳县2018届九年级上学期期末考试数学试卷 题型:解答题
(本题满分12分)如图,在平面直角坐标系xOy中,将抛物线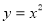 的对称轴绕着点P(
的对称轴绕着点P(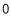 ,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上的一点.
,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上的一点.
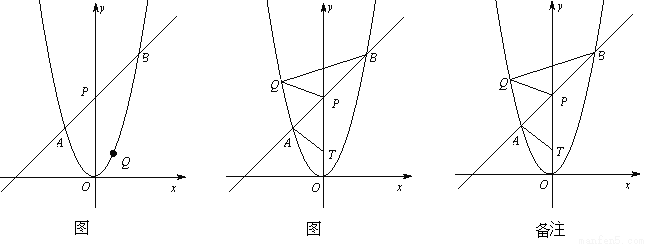
(1)求直线AB的函数表达式;
(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;
(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是直线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值.
(1)y=x+2; (2)当m=时,点Q到直线AB的距离的最大,最大距离为; (3)t=1或t=0或t=1-或t=3-. 【解析】 试题分析:(1)根据题意求出直线AB与坐标轴的交点坐标,用待定系数法即可求解;(2)过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,设Q(m,m2),则C(m,m+2),用m表示出QC的长,再根据QC与QD的关系,构造...查看答案和解析>>
科目: 来源:北师大版九年级上册数学全册综合测试卷二 题型:单选题
已知广州市的土地总面积约为7434km2, 人均占有的土地面积S(单位:km2/人)随全市人口n(单位:人)的变化而变化,则S与n的函数关系式为( )
A. S=7434n B. S=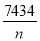 C. n=7434S D. S=
C. n=7434S D. S=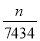
查看答案和解析>>
科目: 来源:北师大版九年级上册数学全册综合测试卷二 题型:单选题
方程x2=3x的根是( )
A. 3 B. -3或0 C. 3或0 D. 0
C 【解析】试题解析:∵x2=3x, ∴x2-3x=0, ∴x(x-3)=0, ∴x=0或x=3, 故选C.查看答案和解析>>
科目: 来源:北师大版九年级上册数学全册综合测试卷二 题型:单选题
如图,若平行四边形ABCD中,AB=6,AD=4,∠B=150°,则平行四边形ABCD的面积为( )
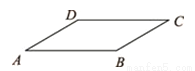
A. 6 B. 12 C. 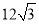 D. 24
D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com