两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，詹姆斯在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO=CO=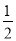AC；③△ABD≌△CBD，其中正确的结论有（　　）

A. 0个 B. 1个 C. 2个 D. 3个

D 【解析】试题解析：在△ABD与△CBD中， ， ∴△ABD≌△CBD（SSS）， 故③正确； ∴∠ADB=∠CDB， 在△AOD与△COD中， ， ∴△AOD≌△COD（SAS）， ∴∠AOD=∠COD=90°，AO=OC， ∴AC⊥DB， 故①②③正确； 故选D．

如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（ ）

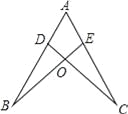
A. ∠B=∠C B. AD=AE C. BD=CE D. BE=CD

D 【解析】试题分析：添加A可以利用ASA来进行全等判定；添加B可以利用SAS来进行判定；添加D选项可以得出AD=AE，然后利用SAS来进行全等判定.

如图,AA',BB'表示两根长度相同的木条,若O是AA',BB'的中点,经测量AB=9 cm,则容器的内径A'B'为(　　)

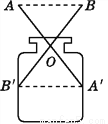
A. 8 cm B. 9 cm C. 10 cm D. 11 cm

B 【解析】【解析】 由题意知：OA=OA′，∠AOB=∠A′OB′，OB=OB′，∴△AOB≌△A′OB′，∴A′B′=AB=9cm．故选B．

如图，已知∠ABC＝∠BAD，添加下列条件还不能判定△ABC≌△BAD的是( )

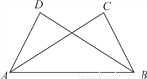
A. AC＝BD B. ∠CAB＝∠DBA

C. ∠C＝∠D D. BC＝AD

A 【解析】试题解析：已知 添加,依据是 添加,依据是 添加,依据是 故选A.

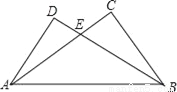
如图，在△ABC和△ABD中，AC与BD相交于点E，AD=BC，∠DAB=∠CBA，求证：AC=BD．

（1）A（﹣3，2）、B（﹣4，﹣3）、C（﹣1，﹣1）； （2）画图见解析； （3）各顶点坐标（﹣3，﹣2）、B（﹣4，3）、C（﹣1，1）． 【解析】试题分析：要证明AC=BD，只需要证明△ADB≌△BAC即可. 试题解析：在△ADB和△BCA中， AD=BC，∠DAB=∠CBA，AB=BA 6分 ∴△ADB≌△BAC（SAS）8分 ∴AC=BD． 9...

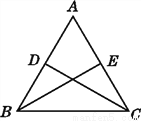
如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.

答案见解析 【解析】试题分析：由中点定义及AB=AC，可得到AD=AE，再通过SAS证明△ADC≌△AEB即可． 试题解析：【解析】 △ADC≌△AEB．理由如下： ∵AB=AC，D，E分别是AB，AC的中点，∴AD=AE． 在△ADC和△AEB中，∵AC=AB，∠A=∠A(公共角)，AD=AE， ∴△ADC≌△AEB(SAS)．

如图，△ABC和△ADE都是等腰三角形，且∠BAC=90°，∠DAE=90°，B，C，D在同一条直线上．求证：BD=CE．

证明：∵△ABC和△ADE都是等腰直角三角形 ∴AD=AE AB=AC 又∵∠EAC=90°+∠CAD， ∠DAB=90°+∠CAD ∴∠DAB=∠EAC 在△ADB和△AEC中 ∴△ADB≌△AEC（SAS） 【解析】试题分析：求出AD=AE，AB=AC，∠DAB=∠EAC，根据SAS证出△ADB≌△AEC即可． 证明：∵△ABC和△ADE都是等腰直角三...

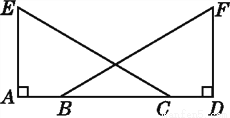
如图,点A,B,C,D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.

试说明:∠ACE=∠DBF.

答案见解析 【解析】试题分析：根据EA⊥AD，FD⊥AD，得出∠EAD=∠FDB，再根据AB=DC得出AC=BD，最后根据SAS证出△EAC≌△FDB，即可得出∠ACE=∠DBF． 试题解析：【解析】 ∵EA⊥AD，FD⊥AD，∴∠EAD=∠FDB=90°． 又∵AB=DC，∴AB+BC=DC+BC，即AC=BD． 在△EAC和△FDB中，∵AE＝DF，∠EAD＝∠FDB...

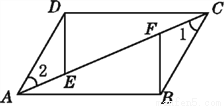
如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF.试说明:BF=DE.

答案见解析 【解析】试题分析：先利用“SSS”证明△ABC≌△CAD，得到∠1=∠2，然后根据“SAS”可判断△BCF≌△DAE，即可得出结论． 试题解析：【解析】 在△ABC和△CDA中，∵AB=CD，BC=DA，CA=AC，∴△ABC≌△CDA(SSS)，∴∠1=∠2(全等三角形的对应角相等)． 在△BCF和△DAE中，∵BC=DA，∠1=∠2，CF=AE，∴△BCF≌△D...

如图,点O是线段AB和线段CD的中点.试说明:

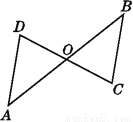
(1)△AOD≌△BOC;

(2)AD∥BC.

(1)答案见解析;(2)答案见解析 【解析】试题分析：（1）由中点定义，得到AO=BO，CO=DO，从而通过SAS证明△AOD≌△BOC； （2）由（1）中结论，可以得到∠A=∠B，再由内错角相等，两直线平行即可得出结论． 试题解析：【解析】 (1)∵点O是线段AB和线段CD的中点，∴AO=BO，CO=DO． 在△AOD和△BOC中，∵AO=BO，∠AOD=∠BOC，DO...