
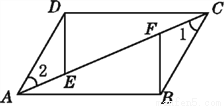
��ͼ,��֪AB=CD,BC=DA,E,F��AC�ϵ�����,��AE=CF.��˵��:BF=DE.
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��2.1.2 ���ߵĶ��������� ͬ����ϰ ���ͣ���ѡ��
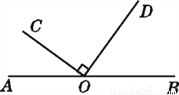
��ͼ,��O��ֱ��AB����OC��OD,����COA=36��,���DOB�Ĵ�СΪ(����)
A. 36�� B. 54�� C. 55�� D. 44��
B ����������OC��OD�����COD��90�㣬�֡ߡ�AOC����COD����DOB��180�㣬���DOB��180�㣭36�㣭90�㣽54�㣮��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²� ��һ�¡���ʽ�ij˳� ��Ԫ���Ծ� ���ͣ���ѡ��
��֪a��b��m��ab����4������(a��2)(b��2)�Ľ����(����)
A. 6 B. 2m��8 C. 2m D. ��2m
D �������������������Ϊ��a��2����b��2��="ab-2a-2b+4=" ab-2��a+b��+4����a+b=m��ab=��4������ԭʽ=-4-2m+4=-2m����ѡ��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��3.2 �ù�ϵʽ��ʾ�ı������ϵ ͬ����ϰ ���ͣ���ѡ��
����y��x֮��Ĺ�ϵʽ��y=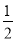 x2+1,���Ա���x=2ʱ,�����y��ֵ��(����)
x2+1,���Ա���x=2ʱ,�����y��ֵ��(����)
A. -2 B. -1 C. 1 D. 3
D ���������ߣ� �൱ʱ�� . ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.3 �á��߽DZߡ��ж�������ȫ�� ͬ����ϰ ���ͣ������
��ͼ,��֪A,D,E���㹲��,C,B,F���㹲��,AB=CD,AD=CB,DE=BF,��ôBE��DF֮����ʲô������ϵ?��˵������.
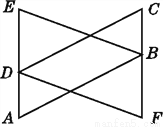
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.3 �á��߽DZߡ��ж�������ȫ�� ͬ����ϰ ���ͣ���ѡ��
��ͼ����֪��ABC����BAD���������������������ж���ABC�ա�BAD����( )
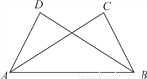
A. AC��BD B. ��CAB����DBA
C. ��C����D D. BC��AD
A �������������������֪ ����,������ ����,������ ����,������ ��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.3 �á��߽DZߡ��ж�������ȫ�� ͬ����ϰ ���ͣ���ѡ��
��ͼ,a,b,c�ֱ��ʾ��ABC�����߳�,���������ABCһ��ȫ�ȵ���������(����)
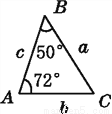
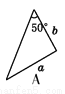
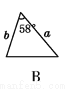
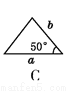
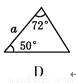
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²������4.4�ó߹��������ο�ʱ��ϰ ���ͣ������
��ͼ��С�������߶�AB�Ĵ�ֱƽ����ʱ�������������ģ��ֱ��Ե�A��BΪԲ�ģ������߶�AB����һ��ij�Ϊ�뾶�������ཻ�ڵ�C��D����ֱ��CD��Ϊ��������AC��BC��AD��BD������������ͼ������֪���ı���ADBCһ���ǣ�____��
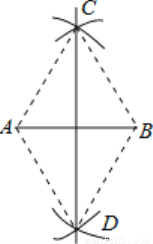
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.1 �á��߱߱ߡ��ж�������ȫ�� ͬ����ϰ ���ͣ���ѡ��
��ʦ����4��ľ������һ���ı���ľ�ܣ���ͼ��Ҫʹ���ľ�ܲ����Σ������ٻ�Ҫ�ٶ��ϼ���ľ������ ��
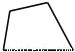
A. 0�� B. 1�� C. 2�� D. 3��
B �������������������ͼ������AC��ԭ���ȶ����ı���ABCD�о������ȶ��ġ�ACD����ABC���������������ݵ��������ε��ȶ��ԣ���ѡB���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com