
科目: 来源:福建省2017-2018学年第二学期期中考试七年级数学试卷 题型:解答题
已知,如图, ,
,


证明:∵ ,
,
∴________________(同旁内角互补,两直线平行),
∴
又∵
∴________________(内错角相等,两直线平行),
∴
∴

即
查看答案和解析>>
科目: 来源:福建省2017-2018学年第二学期期中考试七年级数学试卷 题型:解答题
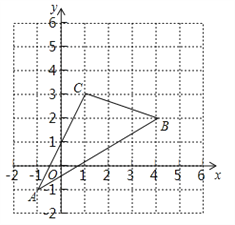
如图,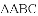
(1)请写出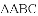
(2)直接写出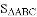 .
.
(3)若把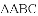
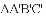
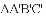
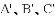
查看答案和解析>>
科目: 来源:福建省2017-2018学年第二学期期中考试七年级数学试卷 题型:解答题
某商场用36万元购进


(1)该商场购进

(2)商场第二次以原进价购进






查看答案和解析>>
科目: 来源:福建省2017-2018学年第二学期期中考试七年级数学试卷 题型:解答题
探究规律:我们有可以直接应用的结论:若两条直线平行,那么在一条直线上任取一点,无论这点在直线的什么位置,这点到另一条直线的距离均相等.例如:如图1,两直线











如图2,已知直线







(1)请写出图中面积相等的各对三角形: .
(2)如果







解决问题:
如图3,五边形


(1)写出设计方案,并在图4中画出相应的图形;
(2)说明方案设计理由.
查看答案和解析>>
科目: 来源:广东省毕业生学业考试数学模拟试卷 题型:单选题
一组数据5,7,8,10,12,12,44的众数和中位数分别是( )
A. 44和10 B. 12和10 C. 10和12 D. 12和11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com