
科目: 来源:浙江省义乌市2018年中考数学试卷 题型:填空题
已知长方体容器的底面是边长为2cm的正方形(高度不限),容器内盛有10cm高的水,现将底面是边长1cm的正方形、高是xcm的长方体铁块竖直放入容器内(铁块全部在水里),容器内的水高y关于x的函数关系式为___________.
查看答案和解析>>
科目: 来源:浙江省义乌市2018年中考数学试卷 题型:解答题
为了解某地区机动机拥有量对道路通行的影响,学校九年级社会实践小组对2010年~2017年机动车拥有量、车辆经过人民路路口和学校门口的堵车次数进行调查统计,并绘制成下列统计图:
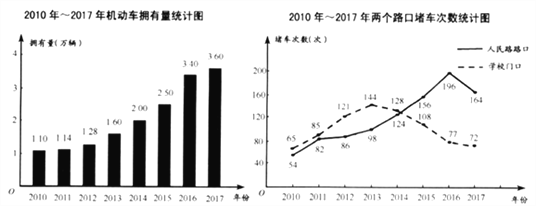
根据统计图,回答下列问题:
(1)写出2016年机动车的拥有量,分别计算2010年~2017年在人民路路口和学校门口堵车次数的平均数.
(2)根据统计数据,结合生活实际,对机动车拥有量与人民路路口和学校门口堵车次数,说说你的看法.
查看答案和解析>>
科目: 来源:浙江省义乌市2018年中考数学试卷 题型:解答题
一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量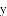
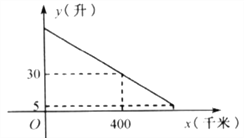
(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求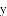
查看答案和解析>>
科目: 来源:浙江省义乌市2018年中考数学试卷 题型:解答题
学校拓展小组研制了绘图智能机器人(如图1),顺次输入点 ,
, ,
, 的坐标,机器人能根据图2,绘制图形.若图形是线段,求出线段的长度;若图形是抛物线,求出抛物线的解析式.请根据以下点的坐标,求出线段的长度或抛物线的函数关系式.
的坐标,机器人能根据图2,绘制图形.若图形是线段,求出线段的长度;若图形是抛物线,求出抛物线的解析式.请根据以下点的坐标,求出线段的长度或抛物线的函数关系式.

(1) ,
, ,
, ;
;
(2) ,
, ,
, .
.
查看答案和解析>>
科目: 来源:浙江省义乌市2018年中考数学试卷 题型:解答题
如图1,窗框和窗扇用“滑块铰链”连接.图3是图2中“滑块铰链”的平面示意图,滑轨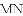
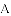
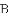
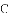
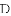
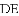
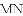
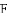
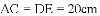
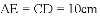
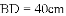
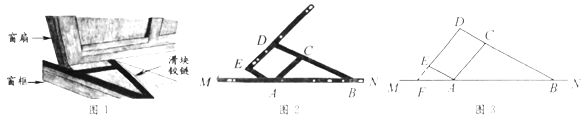
(1)窗扇完全打开,张角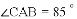 ,求此时窗扇与窗框的夹角
,求此时窗扇与窗框的夹角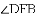
(2)窗扇部分打开,张角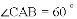 ,求此时点
,求此时点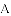
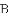
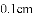
(参考数据: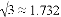 ,
,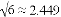 )
)
查看答案和解析>>
科目: 来源:浙江省义乌市2018年中考数学试卷 题型:解答题
数学课上,张老师举了下面的例题:
例1 等腰三角形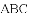
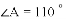 ,求
,求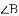
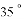 )
)
例2 等腰三角形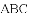
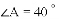 ,求
,求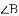
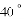 或
或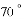 或
或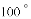 )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形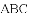
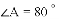 ,求
,求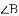
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,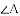
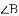
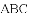
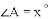 ,当
,当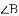
查看答案和解析>>
科目: 来源:浙江省义乌市2018年中考数学试卷 题型:解答题
小敏思考解决如下问题:
原题:如图1,点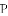
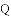
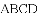
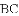
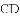
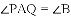
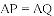
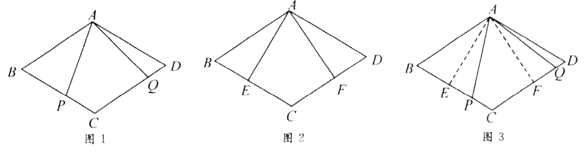
(1)小敏进行探索,若将点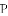
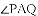
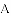
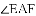
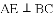
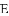
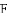
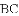
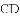

(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作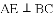
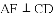
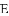
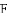
(3)如果在原题中添加条件: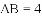
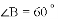 ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
查看答案和解析>>
科目: 来源:浙江省义乌市2018年中考数学试卷 题型:解答题
如图,公交车行驶在笔直的公路上,这条路上有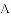



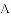


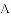
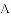

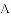


(1)问第一班上行车到

(2)若第一班上行车行驶时间为



(3)一乘客前往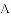









查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com