
科目: 来源:四川省内江市2018年中考数学试卷 题型:填空题
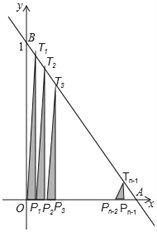
如图,直线y=﹣x+1与两坐标轴分别交于A,B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn﹣1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn﹣1,用S1,S2,S3,…,Sn﹣1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn﹣1Pn﹣2Pn﹣1的面积,则S1+S2+S3+…+Sn﹣1=__________.
查看答案和解析>>
科目: 来源:四川省内江市2018年中考数学试卷 题型:解答题
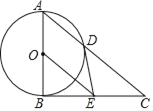
如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CD•OE;
(3)若tanC= ,DE=
,DE= ,求AD的长.
,求AD的长.
查看答案和解析>>
科目: 来源:四川省内江市2018年中考数学试卷 题型:解答题
对于三个数a,b,c,用M{a,b,c}表示这三个数的中位数,用max{a,b,c}表示这三个数中最大数,例如:M{﹣2,﹣1,0}=﹣1,max{﹣2,﹣1,0}=0,max{﹣2,﹣1,a}=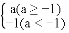
解决问题:
(1)填空:M{sin45°,cos60°,tan60°}=__________,如果max{3,5﹣3x,2x﹣6}=3,则x的取值范围为__________;
(2)如果2•M{2,x+2,x+4}=max{2,x+2,x+4},求x的值;
(3)如果M{9,x2,3x﹣2}=max{9,x2,3x﹣2},求x的值.
查看答案和解析>>
科目: 来源:四川省内江市2018年中考数学试卷 题型:解答题
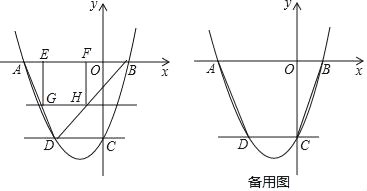
如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.
(1)求抛物线的解析式;
(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H作HF⊥x轴于点F,求矩形GEFH的最大面积;
(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.
查看答案和解析>>
科目: 来源:2017-2018学年泰兴市 初二数学下学期期末试卷 题型:单选题
利用“分形”与“迭代”可以制作出很多精美的图形,以下是制作出的几个简单图形,其中是轴对称但不是中心对称的图形是( )
A.  B.
B.  C.
C. 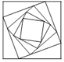 D.
D. 
查看答案和解析>>
科目: 来源:2017-2018学年泰兴市 初二数学下学期期末试卷 题型:单选题
某市今年共有6万名考生参加中考,为了了解这6万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析,以下说法:
①这种调查采用了抽样调查的方式;②6万名考生是总体;
③1000名考生的数学成绩是总体的一个样本;④样本容量是1000名.
其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目: 来源:2017-2018学年泰兴市 初二数学下学期期末试卷 题型:单选题
下列命题中正确的是( )
A. 有一组邻边相等的四边形是菱形
B. 有一个角是直角的平行四边形是矩形
C. 对角线垂直的平行四边形是正方形
D. 一组对边平行的四边形是平行四边形
查看答案和解析>>
科目: 来源:2017-2018学年泰兴市 初二数学下学期期末试卷 题型:单选题
“黄金分割”是一条举世公认的美学定律. 例如在摄影中,人们常依据黄金分割进行构图,使画面整体和谐. 目前,照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗,按照黄金分割的原则,应该使小狗置于画面中的位置( )
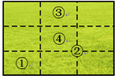
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目: 来源:2017-2018学年泰兴市 初二数学下学期期末试卷 题型:单选题
如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为( )
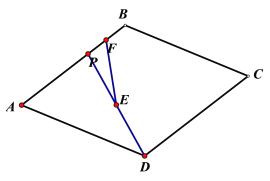
A. 2 B. 4 C. 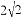 D.
D. 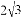
查看答案和解析>>
科目: 来源:2017-2018学年泰兴市 初二数学下学期期末试卷 题型:单选题
如图,点A,B是反比例函数y= (x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA、BC,已知点C(2,0),BD=3,S△BCD=3,则S△AOC为( )
(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA、BC,已知点C(2,0),BD=3,S△BCD=3,则S△AOC为( )
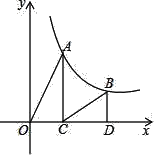
A. 2 B. 3 C. 4 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com