
科目: 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:填空题
如图,长方形ABCD中,AB=4,AD=2.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为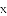
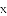
查看答案和解析>>
科目: 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:解答题
如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于直线m对称的△A2B2C2;
(3)在直线m上画一点P,使得 的值最小.
的值最小.

查看答案和解析>>
科目: 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:解答题
一项工程,甲单独做12小时完成,乙单独做8小时完成,甲先单独做9小时,后因甲由其他任务调离,余下的任务由乙单独完成,那么乙还要多少小时完成?
查看答案和解析>>
科目: 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:解答题
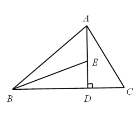
如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若=60°,∠BED=70°.求∠ABC和∠BAC的度数.
查看答案和解析>>
科目: 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:解答题
某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目: 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:解答题
阅读下列材料:
我们知道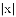 的几何意义是在数轴上数
的几何意义是在数轴上数
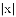 =
=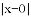 ,也就是说,
,也就是说,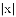 表示在数轴上数
表示在数轴上数
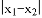 表示在数轴上数
表示在数轴上数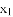 与数
与数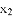 对应的点之间的距离;
对应的点之间的距离;
例1.解方程|
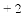

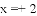
例2.解不等式|








例3.解方程|











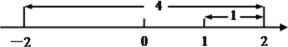
参考阅读材料,解答下列问题:
(1)方程|
(2)解不等式:|
(3)解不等式:|

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com