解不等式组：并写出它的所有的非负整数解．

用适当的方法解二元一次方程组

（1） （2）

先化简，再求值：，求代数式 的值．

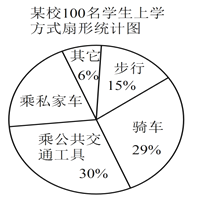
某校有500名学生．为了解全校每名学生的上学方式，该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查．整理样本数据，得到扇形统计图如右图：

（1）本次调查的个体是  ，样本容量是 ；

（2）扇形统计图中，乘私家车部分对应的圆心角是 度；

（3）请估计该校500名学生中，选择骑车和步行上学的一共有多少人?

小明和小丽两人相距8千米，小明骑自行车，小丽步行，两人同时出发相向而行，1小时相遇；若两人同时出发同向而行，小明2小时可以追上小丽，求小明、小丽每小时各走多少千米?

如图，AB∥CD，点O是直线AB上一点，OC平分∠AOF．

（1）求证：∠DCO=∠COF；

（2）若∠DCO=40°，求∠EDF的度数．

为了更好地保护环境，某区污水处理厂决定购买A，B两种型号污水处理设备10台，其中每台的价格、月处理污水量如下表．已知购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

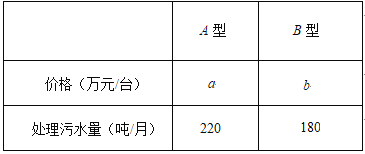
（1）求a，b的值；

（2）某区污水处理厂决定购买污水处理设备的资金既不少于108万元也不超过110万元，问有几种购买方案?每月最多能处理污水多少吨?

小红同学在做作业时，遇到这样一道几何题：

已知：AB∥CD∥EF，∠A＝110°，∠ACE＝100°，过点E作EH⊥EF,垂足为E，交CD于H点．

（1）依据题意，补全图形；

（2）求∠CEH的度数．

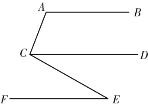
小明想了许久对于求∠CEH的度数没有思路，就去请教好朋友小丽，小丽给了他如图2所示的提示：

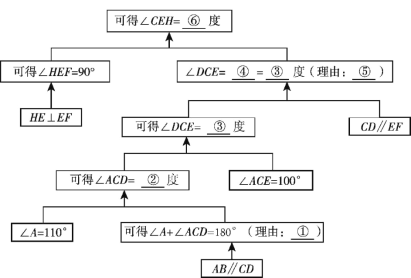
请问小丽的提示中理由①是  ；

提示中②是：  度；

提示中③是：  度；

提示中④是：  ，理由⑤是 ．

提示中⑥是  度；

阅读下列材料：

小明在一本课外读物上看到一道有意思的数学题：例1、解不等式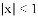：，根据绝对值的几何意义，到原点距离小于1的点在数轴上集中在－1和+1之间，如图:

所以，该不等式的解集为－1<x<1．

因此，不等式的解集为x<－1或x>1．

根据以上方法小明继续探究：例2：求不等式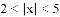：的解集，即求到原点的距离大于2小于5的点的集合就集中在这样的区域内，如图：

所以，不等式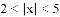的解集为－5<x<－2或2<x<5．

仿照小明的做法解决下面问题：

（1）不等式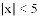的解集为____________．

（2）不等式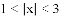的解集是____________．

（3）求不等式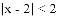的解集．

下面式子是二次根式的是（ ）

A. B. C. D. a