
科目: 来源:黑龙江省哈尔滨市阿城区2018届九年级中考模拟试卷(3月份)数学试卷 题型:解答题
如图网格中每个小正方形的边长均为1,线段AB、CD的端点都在小正方形的顶点上.
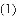
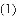
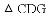
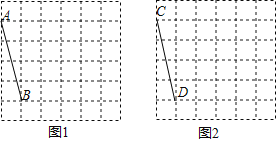
查看答案和解析>>
科目: 来源:黑龙江省哈尔滨市阿城区2018届九年级中考模拟试卷(3月份)数学试卷 题型:解答题
某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目: 来源:黑龙江省哈尔滨市阿城区2018届九年级中考模拟试卷(3月份)数学试卷 题型:解答题
如图,四边形ABCD是正方形,点E、K分别在BC、AB上,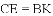
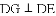
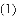
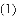
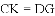
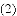
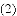
查看答案和解析>>
科目: 来源:黑龙江省哈尔滨市阿城区2018届九年级中考模拟试卷(3月份)数学试卷 题型:解答题
某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支.
(1)求第一批每支钢笔的进价是多少元?
(2)第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折?
查看答案和解析>>
科目: 来源:黑龙江省哈尔滨市阿城区2018届九年级中考模拟试卷(3月份)数学试卷 题型:解答题
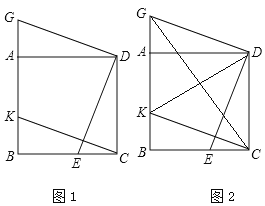
如图,四边形ABCD是
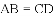
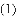
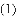
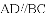
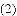
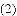
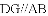
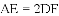
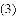
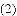
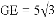 ,
, ,求
,求
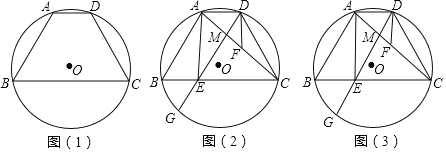
查看答案和解析>>
科目: 来源:黑龙江省哈尔滨市阿城区2018届九年级中考模拟试卷(3月份)数学试卷 题型:解答题
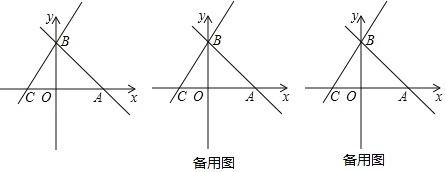
已知:如图,在平面直角坐标系中,直线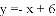
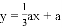 经过点B交x轴于点C.
经过点B交x轴于点C.
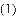
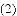
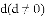
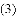
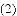
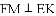
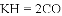
 时,求点D的坐标.
时,求点D的坐标.
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
设关于x的一次函数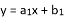 与
与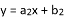 ,则称函数
,则称函数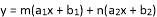 (其中
(其中
(1)当x=1时,求函数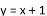

(2)若函数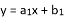 与
与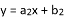 的图象的交点为
的图象的交点为
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
武警战士乘一冲锋舟从
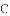
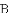
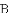
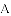
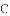
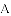
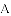
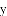
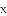
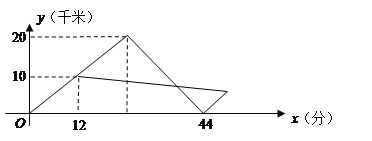
(1)请直接写出冲锋舟从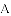
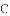
(2)求水流的速度.
(3)冲锋舟将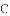
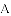
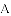
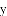
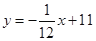 ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
如图,在平面直角坐标系中,函数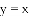

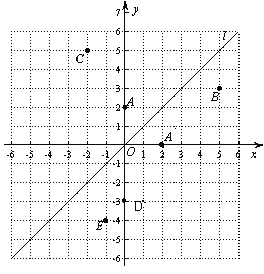
实验与探究:由图观察易知A(0,2)关于直线

归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线
 的坐标为____________;
的坐标为____________;
运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com