
科目: 来源:2018-2019学年度第一学期新人教版九年级数学上册_第22章_二次函数_单元检测试卷 题型:填空题
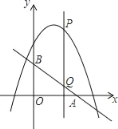
如图,已知直线y=﹣ x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣ x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣ x+3于点Q,则当PQ=BQ时,a的值是_____.
x+3于点Q,则当PQ=BQ时,a的值是_____.
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期新人教版九年级数学上册_第22章_二次函数_单元检测试卷 题型:填空题
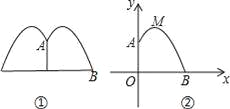
如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处M(1,2.25),如果不考虑其他因素,那么水池的半径至少要______m,才能使喷出的水流不至落到池外.
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期新人教版九年级数学上册_第22章_二次函数_单元检测试卷 题型:解答题
已知函数y=(k﹣2)xk²﹣4k+5+2x是关于x的二次函数.求:
(1)满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点,这时,x为何值时,y随x的增大而增大?
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期新人教版九年级数学上册_第22章_二次函数_单元检测试卷 题型:解答题
如图,在某场足球比赛中,球员甲从球门底部中心点
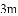
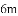
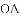
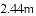
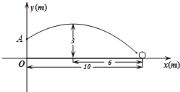
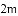
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期新人教版九年级数学上册_第22章_二次函数_单元检测试卷 题型:解答题
如图,抛物线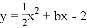 与
与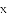
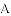
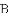
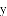
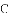
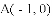
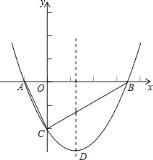
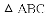
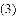
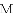
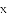
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期新人教版九年级数学上册_第22章_二次函数_单元检测试卷 题型:解答题
在平面直角坐标系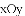
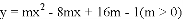 与
与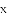
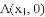 ,
,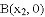 .
.
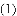
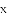
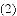
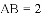
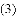
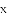
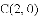
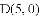
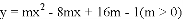 与线段
与线段
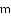
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期新人教版九年级数学上册_第22章_二次函数_单元检测试卷 题型:解答题
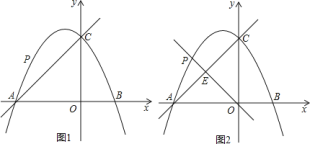
在平面直角坐标系中,抛物线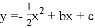 与
与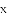
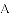
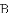
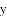
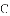
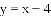
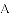
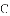
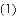
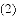
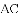
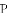
①如图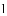
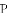
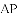
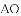
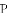
②如图
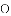
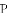
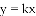
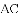
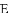
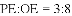
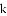
查看答案和解析>>
科目: 来源:山东省2019届第一学期北师大版九年级数学上第二章一元二次方程周末自主测评试卷 题型:单选题
若

 有一根是( )
有一根是( )
A. 1 B. -1 C. 0 D. 无法判断
查看答案和解析>>
科目: 来源:山东省2019届第一学期北师大版九年级数学上第二章一元二次方程周末自主测评试卷 题型:单选题
方程 的一般形式是( )
的一般形式是( )
A.  -6x+4=5 B.
-6x+4=5 B.  -6x-4=5
-6x-4=5
C.  -6x-1=0 D.
-6x-1=0 D.  -6x-9=0
-6x-9=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com