
科目: 来源:月考题 题型:解答题

查看答案和解析>>
科目: 来源:北京期末题 题型:解答题
查看答案和解析>>
科目: 来源:同步题 题型:解答题
 表示。
表示。
查看答案和解析>>
科目: 来源:四川省中考真题 题型:解答题
 ,那么结论OF=
,那么结论OF= DG能成立吗?请说明理由;
DG能成立吗?请说明理由;
查看答案和解析>>
科目: 来源:专项题 题型:解答题
查看答案和解析>>
科目: 来源:专项题 题型:解答题

查看答案和解析>>
科目: 来源:专项题 题型:解答题
 )
) 
查看答案和解析>>
科目: 来源:湖南省中考真题 题型:解答题
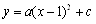 与
与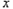 轴交于点A(
轴交于点A(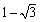 ,0)和点B,将抛物线沿
,0)和点B,将抛物线沿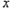 轴向上翻折,顶点P落在点P'(1,3)处.
轴向上翻折,顶点P落在点P'(1,3)处.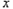
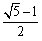 轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W,“5W,“W,寓意深远;而且小明通过计算惊奇的发现这个“W(CD)的比非常接近黄金分割比(约等于0.618).请你计算这个“W?(参考数据:
轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W,“5W,“W,寓意深远;而且小明通过计算惊奇的发现这个“W(CD)的比非常接近黄金分割比(约等于0.618).请你计算这个“W?(参考数据: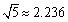
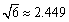 结果可保留根号)
结果可保留根号)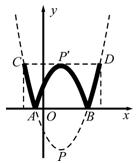
查看答案和解析>>
科目: 来源:专项题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com