
科目: 来源:同步题 题型:解答题

查看答案和解析>>
科目: 来源:上海期末题 题型:解答题
 ,线段OA、OB的长是关于x的一元二次方程
,线段OA、OB的长是关于x的一元二次方程 的两个根.
的两个根. 
查看答案和解析>>
科目: 来源:湖南省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:北京期末题 题型:解答题
| 如图,有一座抛物线形的拱桥,桥下面处在目前的水位时,水面宽AB=10m,如果水位上升2m,就将达到警戒线CD,这时水面的宽为8m.若洪水到来,水位以每小时0.1m 速度上升,经过多少小时会达到拱顶? |
 |
查看答案和解析>>
科目: 来源:海南省月考题 题型:解答题

查看答案和解析>>
科目: 来源:宁夏自治区月考题 题型:解答题
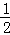 ah,即三角形面积等于水平宽与铅垂高乘积的一半。
ah,即三角形面积等于水平宽与铅垂高乘积的一半。 S△CAB?若存在,求出P点的坐标;若不存在,请说明理由。
S△CAB?若存在,求出P点的坐标;若不存在,请说明理由。

查看答案和解析>>
科目: 来源:新疆自治区期中题 题型:解答题
查看答案和解析>>
科目: 来源:福建省中考真题 题型:解答题
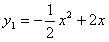
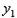 的顶点坐标.
的顶点坐标. 线
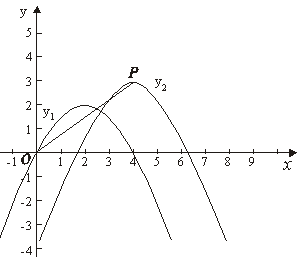
线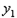 向右平移2个单位,再向上平移1个单位,得到抛物线
向右平移2个单位,再向上平移1个单位,得到抛物线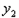 ,求抛物线
,求抛物线 的解析式.
的解析式.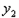 的顶点为P,
的顶点为P,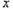 轴上有一动点M,在
轴上有一动点M,在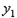 、
、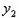 这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形,若存在,求出N点的坐标;若不存在,请说明理由
这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形,若存在,求出N点的坐标;若不存在,请说明理由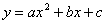 (
(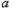 ≠0)的对称轴是
≠0)的对称轴是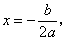 顶点坐标是
顶点坐标是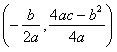 ]
]
查看答案和解析>>
科目: 来源:广西自治区中考真题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com