科目： 来源：江苏期中题 题型：解答题

已知二次函数
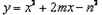
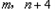（1）若此二次函数的图象经过点（1，1），且记两数中较大者为P，试求P关于n的函数关系式，并说明P的最小值．
（2）若变化时，它们的图象是不同的抛物线，如果每条抛物线与坐标轴都有三个不同的交点，过这三个交点作圆，请说明这些圆都经过同一定点，并求出这个定点的坐标．

科目： 来源：江苏期中题 题型：解答题

如图，OB是矩形OABC的对角线，抛物线y＝-x＋x＋6经过B、C两点。
（1）求点B的坐标；
（2）D、E分别是OC、OB上的点，OD＝5，OE＝2EB，过D、E的直线交x轴于F，试说明OE⊥ DF；
（3）若点M是（2）中直线DE上的一个动点，在x轴上方的平面内是否存在另一个点N，使以O、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由。

科目： 来源：河北省期末题 题型：解答题

如图，已知二次函数y=﹣x²+bx+c的图象经过A（2，0）、B（0，﹣6）两点．
（1）求这个二次函数的解析式．
（2）设该二次函数的对称轴与x轴交于点C，连结BA、BC，求△ABC的面积．

科目： 来源：河北省期末题 题型：解答题

如图，已知点A（3，0），以A为圆心作⊙A与y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l．
（1）以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；
（2）抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求DE的长；
（3）点F是切线DE上的一个动点，当△BFD与△EAD相似时，求出BF的长．

科目： 来源：河北省期末题 题型：解答题

如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸．A型、B型、C型三种墙纸的单价分别为每平方米
60元、80元、40元．
（1）如果木板边长为2米，FC=1米，则一块木板用墙纸的费用需要                   元．
（2）如果木板边长为1米，设正方形EFCG的边长为x（米）时，墙纸费用为y（元），求y与x的函数关系式；并求出当正方形EFCG的边长为多少时，墙纸费用最省；最省的费用为多少？

科目： 来源：湖南省月考题 题型：解答题

要修一个圆形喷水池，在池中心竖直安装一根水管，水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？

科目： 来源：湖南省月考题 题型：解答题

在直角坐标平面内，二次函数图象的顶点为A（1，﹣4），且过点B（3，0）．
（1）求该二次函数的解析式；
（2）将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点？并直接写出平移后所得图象与x轴的另一个交点的坐标．