科目： 来源：期中题 题型：填空题

科目： 来源：期中题 题型：填空题

科目： 来源：期中题 题型：填空题

科目： 来源：重庆市期中题 题型：解答题

重庆市的重大惠民工程--公租房建设已陆续竣工，计划10年内解决低收入人群的住房问题，前6年，每年竣工投入使用的公租房面积y （单位：百万平方米），与时间x的关系是y=x+5，（x单位：年，1≤x≤6且x为整数）；后4年，每年竣工投入使用的公租房面积y（单位：百万平方米），与时间x的关系是y=（x单位：年，7≤x≤10且x为整数）。假设每年的公租房全部出租完．另外，随着物价上涨等因素的影响，每年的租金也随之上调，预计，第x年投入使用的公租房的租金z（单位：元/m2）与时间x（单位：年，1≤x≤10且x为整数）满足一次函数关系如下表：

z（元/m2） 50 52 54 56 58 … x（年） 1 2 3 4 5 … （1）求出z与x的函数关系式； （2）求政府在第几年投入的公租房收取的租金最多，最多为多少百万元； （3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年投入的公租房总面积不变的情况下，要让人均住房面积比第6年人均住房面积提高a%，这样可解决住房的人数将比第6年减少1.35a%，求a的值。 （参考数据：）

科目： 来源：江苏省期中题 题型：解答题

如图，直角梯形OABC中，∠COA=90°，BC∥OA，OA=6，BC=3，AB=，已知抛物线经过O、A、B三点。

（1）求抛物线的解析式；
（2）平行与y轴的直线l从点O向终点A匀速运动，速度是每秒1个单位长，运动时间为t秒。直线l交折线段OBA于点D，交抛物线于点E，问：当t为何值时，线段DE有最大值？最大值是多少？
（3）探索：坐标平面内是否存在一点F，使得以C、B、D、F为顶点的四边形是菱形？如果存在，请直接写出点F的坐标；如果不存在，请说明理由。

科目： 来源：江苏省期中题 题型：解答题

科目： 来源：江苏省期中题 题型：解答题

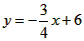直线与坐标轴分别交于A，B两点，动点P、Q同时从O点出发，同时到达A点，运动停止。点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O→B→A运动。
（1）直接写出A，B两点的坐标；
（2）设点Q的运动时间为t秒，△OPQ的面积为S，求出S与t之间的函数关系式；
（3）试探讨在运动过程中线段PQ会不会与△AOB的某条边平行，如果会，请求出此时的时间t；如果不会，试说明理由。

科目： 来源：期末题 题型：解答题

如图，在平面直角坐标系中，已知OA=12cm，OB=6cm，点P从点O开始沿OA边向点A以1厘米/秒的速度移动，点Q从点B开始沿BO边向点O以1厘米/秒的速度移动，如果P、Q同时出发，用t秒表示移动的时间（），那么
（1）设△POQ的面积为y（厘米²），求y关于t（秒）的函数解析式；
（2）当t=3时，将△POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由；
（3）当t为何值时，以O、P、Q为顶点的三角形与△AOB相似？

科目： 来源：期末题 题型：解答题

如图，在直角梯形OABC中，已知B、C两点的坐标分别为B（8，6）、C（10，0），动点M由原点O出发沿OB方向匀速运动，速度为1单位/秒；同时，线段DE由CB出发沿BA方向匀速运动，速度为1单位/秒，交OB于点N，连接DM，过点M作MH⊥AB于H，设运动时间为t（s）（0＜t＜8），
（1）试说明：△BDN∽△OCB ；
（2）试用t的代数式表示MH的长；
（3）当t为何值时，以B、D、M为顶点的三角形与△OAB相似？
（4）设△DMN的面积为y，求y与t之间的函数关系式。

科目： 来源：期中题 题型：解答题