
科目: 来源:四川省中考真题 题型:填空题
查看答案和解析>>
科目: 来源:四川省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:四川省中考真题 题型:解答题
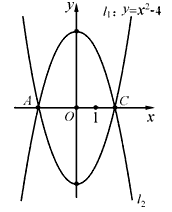
查看答案和解析>>
科目: 来源:期末题 题型:解答题
 ,△ABC的面积为8。
,△ABC的面积为8。
查看答案和解析>>
科目: 来源:吉林省期末题 题型:解答题
 图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、C两点的横坐标分别为1和4。
图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、C两点的横坐标分别为1和4。
查看答案和解析>>
科目: 来源:江苏中考真题 题型:解答题
 中,点P为函数
中,点P为函数 在第一象限内的图象上的任一点,点A的坐标为
在第一象限内的图象上的任一点,点A的坐标为 ,直线
,直线 过
过 且与x轴平行,过
且与x轴平行,过 作y轴的平行线分别交x轴,
作y轴的平行线分别交x轴, 于
于 ,连结
,连结 交x轴于H,直线
交x轴于H,直线 交y轴于R.
交y轴于R. 的中点;
的中点; 为平行四边形; ②平行四边形
为平行四边形; ②平行四边形 为菱形;
为菱形; 有无其它公共点?并说明理由.
有无其它公共点?并说明理由. 
查看答案和解析>>
科目: 来源:广西自治区中考真题 题型:单选题

查看答案和解析>>
科目: 来源:吉林省期末题 题型:解答题
 ,O为斜边BC的中点,点P由点A出发沿线段AB作匀速运动,P′是P关于AO的对称点;点Q由点O出发沿射线OC方向作匀速运动,且满足四边形QOPP′是平行四边形,设平行四边形QOPP′的面积为y,OQ=x。
,O为斜边BC的中点,点P由点A出发沿线段AB作匀速运动,P′是P关于AO的对称点;点Q由点O出发沿射线OC方向作匀速运动,且满足四边形QOPP′是平行四边形,设平行四边形QOPP′的面积为y,OQ=x。
查看答案和解析>>
科目: 来源:山西省中考真题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com