
科目: 来源:北京模拟题 题型:解答题
 和2。
和2。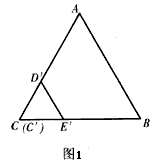


查看答案和解析>>
科目: 来源:北京期中题 题型:解答题
查看答案和解析>>
科目: 来源:山东省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:山东省中考真题 题型:单选题
[ ]
查看答案和解析>>
科目: 来源:内蒙古自治区中考真题 题型:单选题
 的一部分,如图所示,若命中篮圈中心,则他与篮底的距离L是
的一部分,如图所示,若命中篮圈中心,则他与篮底的距离L是
[ ]
查看答案和解析>>
科目: 来源:山东省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:内蒙古自治区中考真题 题型:解答题

查看答案和解析>>
科目: 来源:山东省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:内蒙古自治区中考真题 题型:解答题
 ,AD=1,点P在AC上,PQ⊥BP,交CD于Q,PE⊥CD,交于CD于E,点P从A点(不含A)沿AC方向移动,直到使点Q与点C重合为止。
,AD=1,点P在AC上,PQ⊥BP,交CD于Q,PE⊥CD,交于CD于E,点P从A点(不含A)沿AC方向移动,直到使点Q与点C重合为止。
查看答案和解析>>
科目: 来源:山东省中考真题 题型:单选题

[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com