
科目: 来源:重庆市中考真题 题型:解答题

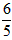 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;查看答案和解析>>
科目: 来源:模拟题 题型:解答题
心理学家研究发现,一般情况下,学生的注意力随着教师讲课时间的变化而变化,讲课开始时,学生的注意力逐渐增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散,经过实验分析可知,学生的注意力y,随时间t的变化规律有如下关系式: 
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中?
(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目: 来源:模拟题 题型:解答题
 上的动点(不与点A、D 重合),直线CG交x轴于点P。
上的动点(不与点A、D 重合),直线CG交x轴于点P。
查看答案和解析>>
科目: 来源:模拟题 题型:解答题
查看答案和解析>>
科目: 来源:湖北省中考真题 题型:解答题

查看答案和解析>>
科目: 来源:模拟题 题型:解答题
 。
。
查看答案和解析>>
科目: 来源:浙江省中考真题 题型:解答题
 与x轴交与点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点,直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q。
与x轴交与点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点,直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q。
查看答案和解析>>
科目: 来源:内蒙古自治区中考真题 题型:解答题
 ,且△AOB∽△BOC。
,且△AOB∽△BOC。
查看答案和解析>>
科目: 来源:模拟题 题型:解答题
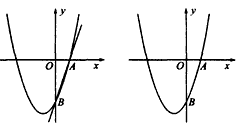
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com