
科目: 来源:期末题 题型:解答题
查看答案和解析>>
科目: 来源:期末题 题型:解答题

查看答案和解析>>
科目: 来源:期末题 题型:解答题

查看答案和解析>>
科目: 来源:期末题 题型:解答题

查看答案和解析>>
科目: 来源:北京期末题 题型:解答题
 轴相交于点B、C(点B在点C的左边),与
轴相交于点B、C(点B在点C的左边),与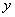 轴相交于点D、M(点D在点M的下方)。
轴相交于点D、M(点D在点M的下方)。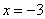 为对称轴,且经过点D、C的抛物线的解析式;
为对称轴,且经过点D、C的抛物线的解析式; 查看答案和解析>>
科目: 来源:重庆市期中题 题型:解答题
 万元. 为了响应我国西部大开发的宏伟决策,镇政府在制定经济发展的10年规划时,拟定开发花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路;后5年公路修通时,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每年固定投资x万元可获利润
万元. 为了响应我国西部大开发的宏伟决策,镇政府在制定经济发展的10年规划时,拟定开发花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路;后5年公路修通时,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每年固定投资x万元可获利润 万元.
万元. 
 ,计算结果保留1位小数)
,计算结果保留1位小数) 查看答案和解析>>
科目: 来源:福建省期中题 题型:解答题

查看答案和解析>>
科目: 来源:福建省中考真题 题型:解答题
查看答案和解析>>
科目: 来源:福建省中考真题 题型:解答题
 与x轴交于A(1,0)、 B(5,0)两点.
与x轴交于A(1,0)、 B(5,0)两点. 
 ).
). ,求s与t之间的函数关系式.
,求s与t之间的函数关系式. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com