
科目: 来源:同步题 题型:填空题

查看答案和解析>>
科目: 来源:同步题 题型:填空题

查看答案和解析>>
科目: 来源:同步题 题型:解答题

查看答案和解析>>
科目: 来源:同步题 题型:解答题
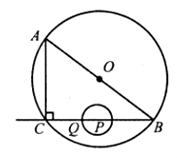
如图,在Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
(1)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
(2)已知圆O为△ABC的外接圆,若OP与圆O相切,求t的值.
查看答案和解析>>
科目: 来源:同步题 题型:解答题
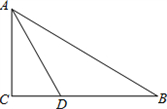
 ,求线段 BD、BE 与劣弧DE所围成的图形面积. (结果保留根号和π)
,求线段 BD、BE 与劣弧DE所围成的图形面积. (结果保留根号和π)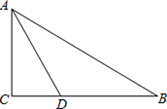
查看答案和解析>>
科目: 来源:同步题 题型:解答题

查看答案和解析>>
科目: 来源:同步题 题型:解答题
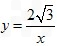 (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A。
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A。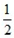 ,若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
,若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.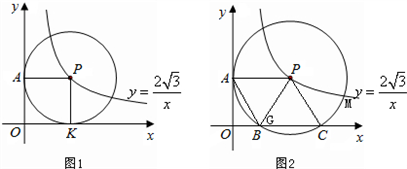
查看答案和解析>>
科目: 来源:同步题 题型:解答题
 + bx +c经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1,
+ bx +c经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com