练习册

  • 练习册
  • 试题
    相关习题
     0  60178  60186  60192  60196  60202  60204  60208  60214  60216  60222  60228  60232  60234  60238  60244  60246  60252  60256  60258  60262  60264  60268  60270  60272  60273  60274  60276  60277  60278  60280  60282  60286  60288  60292  60294  60298  60304  60306  60312  60316  60318  60322  60328  60334  60336  60342  60346  60348  60354  60358  60364  60372  366461 

    科目： 来源：浙江省期末题 题型：解答题

    如图，BC为半圆的直径，O为圆心， D是AC弧的中点，四边形ABCD的对角线AC，BD交于点E。
    （l）△ABE与△DBC是否相似，并请你说明理由；
    （2）若BC=，CD=，求sin∠AEB的值。

    查看答案和解析>>

    科目： 来源：期末题 题型：操作题

    如图，在平面直角坐标系中，已知△ABC，点P（1，2）
    （1）作△PQR，使△PQR与△ABC相似（不要求写出作法）；
    （2）在第（1）小题所作的图形中，求△PQR与△ABC的周长比

    查看答案和解析>>

    科目： 来源：同步题 题型：解答题

    如图所示，E是正方形ABCD的边AB上的动点， EF⊥DE交BC 于点F。
    （1）求证：△ADE∽△BEF；
    （2）设正方形的边长为4，AE=x，BF=y。当x取什么值时， y有最大值？并求出这个最大值．

    查看答案和解析>>

    科目： 来源：模拟题 题型：解答题

    在Rt△ABC和Rt△A′B′C′中，∠ACB=∠A′C′B′=90°．
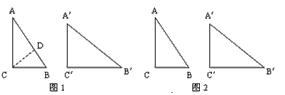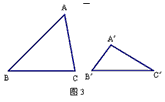    （1）如图1，分割线CD将Rt△ABC分割成两个三角形△ADC和△BDC，且满足∠BCD=∠B′．试在Rt△A′B′C′的内部也作一条类似的分割线，使这条分割线把Rt△A′B′C′分得的两个三角形分别与△ADC和△BDC相似，并说明你画法的正确性（作图工具不限，下同）；
    （2）请在图2中画出与图1中不同的两条分割线，使得Rt△ABC被分得的两个三角形与Rt△A′B′C′被分得的两个三角形分别相似（直接画出分割线，写出相似三角形，不必说明理由）；
    （3）如图3，已知任意△ABC和△A′B′C′，试分别在△ABC和△A′B′C′中画1条或两条分割线，使得△ABC被分得的若干个三角形分别与△A′B′C′被分得的若干个三角形相似（直接画出分割线，相等的角分别在图中用∠1、∠1′，∠2、∠2′，∠3、∠3′，……对应地标明，并写出所有相似三角形，不必说明理由）．
    （4）由上面的操作，你得到什么一般性的经验?

    查看答案和解析>>

    科目： 来源：月考题 题型：单选题

    下列各组图形中有可能不相似的是
    [     ]
    A、各有一个角是105°的等腰三角形
    B、各有一个角是90°的等腰三角形
    C、各有一个角是60°的等腰三角形
    D、各有一个角是30°的等腰三角形

    查看答案和解析>>

    科目： 来源：江苏期中题 题型：单选题

    如图，D、E分别是△ABC的AB、AC是的点，则下列条件不能判定△ADE与△ABC相似的是
    [     ]
    A．∠B=∠ADE
    B．AD：AE=AB：AC
    C．AD：DE=AB：BC
    D．DE∥BC

    查看答案和解析>>

    科目： 来源：海南省期末题 题型：解答题

    如图，在矩形ABCD中，AB =6，AD =11。直角尺的直角顶点P在AD上滑动时（点P与A，D不重合），一直角边始终经过点C，另一直角边与AB交于点E。
    （1）△CDP与△PAE相似吗？如果相似，请写出证明过程；
    （2）当∠PCD =30°时，求AE的长；
    （3）是否存在这样的点P，使△CDP的周长等于△PAE周长的2倍？若存在，求DP的长；若不存在，请说明理由。

    查看答案和解析>>

    科目： 来源：北京期末题 题型：解答题

    数学活动课上，甲、乙两位同学在研究一道数学题：“已知：如图1，在ΔABC和ΔDEF中，∠A=∠D=
    90°，∠B=50°，∠E=32°，且BC=EF，试画出直线m，l，使直线m将ΔABC分成的两个小三角形与直线l将ΔDEF分成的两个小三角形分别相似，并标出每个小三角形各内角的度数。”
    甲同学是这样做的：如图2，使得两个直角三角形的斜边重合，以斜边中点O为圆心，OB长为半径作出辅助圆，根据到定点的距离等于定长的点在圆上，可知A、B（E）、C（F）、D在⊙O上。设BD所在的直线m与AC所在的直线l交于点G，根据同弧所对的圆周角相等，由∠ABC=50°，∠DEF=32°，易求得∠ABG=∠DFG=18°，再由∠A=∠D=90°，可求得∠AGB=∠DGF=72°，∠GCB=40°，∠BGC=
    108°，从而ΔAGB~ΔDGF，ΔGBC~ΔGEF。
    乙同学在甲同学的启发下，利用辅助圆又补充了其它分割方法。你看明白甲同学的分割方法了吗？请你仿照甲同学的方法，把这道题其它的所有分割方法补充完整。
    要求：不需写解答过程，如图2所示，利用辅助圆画出示意图，标明直线及每个小三角形各内角的度数即可。

    查看答案和解析>>

    科目： 来源：江苏期中题 题型：操作题

    在5×5正方形网格中，如图1，有格点△ABC，试在另外三个网格中各画出一个与△ABC相似的格点三角形（要求相似比各不相同且与△ABC的相似比不为1）．

    图1                    图2                    图3                    图4

    查看答案和解析>>

    科目： 来源：江苏期中题 题型：解答题

    如图矩形ABCD中，E为BC上一点，DF⊥AE于F．
    （1）求证：△ABE∽△DFA；
    （2）若AB=6 ，AD=12 ，BE=8，求DF的长．

    查看答案和解析>>

    同步练习册答案