
科目: 来源:同步题 题型:单选题
 ,则点B1的坐标是
,则点B1的坐标是 
[ ]
查看答案和解析>>
科目: 来源:同步题 题型:单选题
 连接各点所得图形与原图形相比
连接各点所得图形与原图形相比
查看答案和解析>>
科目: 来源:广西自治区期末题 题型:单选题

查看答案和解析>>
科目: 来源:山东省同步题 题型:单选题
 =k②ΔBCD∽ΔB′C′D′ ③
=k②ΔBCD∽ΔB′C′D′ ③ ④
④
查看答案和解析>>
科目: 来源:福建省期中题 题型:单选题
查看答案和解析>>
科目: 来源:同步题 题型:单选题
 ,横坐标不变
,横坐标不变 查看答案和解析>>
科目: 来源:同步题 题型:操作题

查看答案和解析>>
科目: 来源:同步题 题型:操作题

查看答案和解析>>
科目: 来源:同步题 题型:解答题
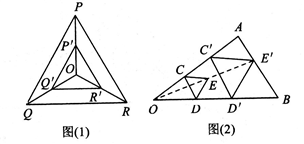
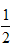 、点P
、点P 、点O
、点O查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com