Question

在正方体AC₁中,M、N分别为棱AA₁和BB₁的中点，若θ为CM与D₁N所成的角，则sinθ的值为（    ）

A.                   B.                  C.                D.

Answer 1

D

解法一：以D为原点建立空间直角坐标系:

设正方体棱长为1,则:D(0,0,0),M(1,0,),

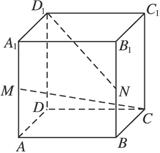
C(0,1,0),N(1,1,),D₁(0,0,1).

=(1,-1,),=(1,1,-)，

·=1-1-=-，||==，||==，

∴cos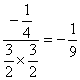＜, ＞.sin＜,＞=.

解法二：取D₁D的中点为E.

连结ME、MB、EC,则四边形BMEC为矩形.连结BE，则MC、BE是矩形BMEC的对角线，

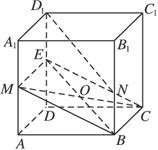
又BND₁EBB₁，

∴四边形BND₁E是平行四边形.

∴D₁NBE,则BE与CM所成的角就是D₁N与CM所成的角.

设MC与BE交于O，正方体和棱长为2，则MC=BE=D₁N=3.

OE=OM=.

在△MOE中，

cosMOE=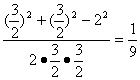·sin∠MOE=.

即∠MOE是CM与D₁M所成的角θ,

∴sinθ=.