
 ijͳ�Ʋ��ž͡�A�������۸�����Ĺ�����Ը����100�˽������ʾ����飬�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ����֪����������������[10��15���ϵ�����������������[25��30��������֮��Ϊ3��4��
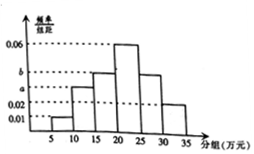
ijͳ�Ʋ��ž͡�A�������۸�����Ĺ�����Ը����100�˽������ʾ����飬�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ����֪����������������[10��15���ϵ�����������������[25��30��������֮��Ϊ3��4������ ����������������������[10��15���ϵ�����������������[25��30���������ֱ�Ϊ3k��4k������Ƶ�ʷֲ�ֱ��ͼ���k���ɴ������a��b��ֵ��
������Ƶ�ʷֲ�ֱ��ͼ����������[5��20���ڵ�Ƶ��Ϊ0.4����������[20��25���ڵ�Ƶ��Ϊ0.3���ɴ������A�������۸����乺����Ը����λ����
�����ֲ�����ķ�������������[10��15����[20��25���Ͻ��ܵ����������ѡȡ6�˲μ���̸������������[10��15����ѡȡ2�ˣ�[20��25����ѡȡ4�ˣ��ɴ����ö����¼����ʼ��㹫ʽ�������[10��15����������������һ�˱�ѡ�еĸ��ʣ�
��� �⣺����������������������[10��15���ϵ�����������������[25��30���������ֱ�Ϊ3k��4k��
��$\left\{\begin{array}{l}{��0.01+a+b+0.06+b+0.02����5=1}\\{0.03k+0.04k+0.04k=1-��0.01+0.06+0.02����5}\end{array}\right.$��
���k=5����a=0.03k��5=0.03��b=0.04k��5=0.04��
������Ƶ�ʷֲ�ֱ��ͼ����������[5��20���ڵ�Ƶ��Ϊ����0.01+0.03+0.04����5=0.4��
��������[20��25���ڵ�Ƶ��Ϊ��0.06��5=0.3��
��A�������۸����乺����Ը����λ��Ϊ��
20+$\frac{0.5-0.4}{0.3}��5$=$\frac{65}{3}$��
�����ֲ�����ķ�������������[10��15����[20��25���Ͻ��ܵ����������ѡȡ6�˲μ���̸��
������������[10��15����ѡȡ��6��$\frac{0.03}{0.03+0.06}$=2�ˣ�[20��25����ѡȡ��6��$\frac{0.06}{0.03+0.06}$=4�ˣ�
����6�������ѡȡ2����Ϊ��Ҫ�����ˣ�
�����¼�����n=${C}_{6}^{2}=15$��
��[10��15����������������һ�˱�ѡ�еĶ����¼���ѡ�е�2�˶���[20��25���ڣ�
����[10��15����������������һ�˱�ѡ�еĸ���p=1-$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{3}{5}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ�������ֲ������Ӧ�ã�������λ����������������֤��������������������������ν��˼�롢ת������˼�룬���е��⣮


 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
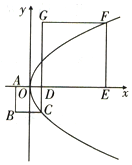 ��ͼ��ʾ��������ABCD��������DEFG��ԭ��OΪAD���е㣬������y2=2px��p��0������C��F���㣬��ֱ��BE��б��Ϊ��������
��ͼ��ʾ��������ABCD��������DEFG��ԭ��OΪAD���е㣬������y2=2px��p��0������C��F���㣬��ֱ��BE��б��Ϊ��������| A�� | $\frac{{\sqrt{2}}}{2}$ | B�� | $1-\frac{{\sqrt{2}}}{2}$ | C�� | $2+\sqrt{2}$ | D�� | $2-\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{30}$ | B�� | $\frac{5\sqrt{3}}{2}$ | C�� | 4$\sqrt{2}$ | D�� | 3$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����f��x��=|3x-4|��
��֪����f��x��=|3x-4|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com