
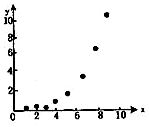
 如图所示的散点图,现选用两种回归模型,模型A:使用线性回归,计算相关指数$R_1^2$;模型B:用指数回归,计算出相关指数$R_2^2$,则一定有( )
如图所示的散点图,现选用两种回归模型,模型A:使用线性回归,计算相关指数$R_1^2$;模型B:用指数回归,计算出相关指数$R_2^2$,则一定有( )| A. | $R_1^2>R_2^2$ | B. | $R_1^2<R_2^2$ | C. | $R_1^2=R_2^2$ | D. | 无法确定 |
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 命题“?x∈R,ax+b≤0”的否定是“?x0∈R,ax0+b>0” | |
| C. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| D. | 命题“若p,则¬q”为真命题,则“若q,则¬p”也为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-4)∪(-4,1] | D. | (-∞,-4)∪(-4,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+=0或2x-y-=0 | B. | 2x+y+=0或2x+y-=0 | ||
| C. | 2x-y+5=0或2x-y-5=0 | D. | 2x+y+5=0或2x+y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<0或0<x<$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-1,-\frac{1}{4})$ | B. | $(-1,-\frac{1}{4}]$ | C. | (-1,+∞) | D. | $(-∞,-\frac{1}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
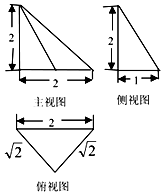
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 9 | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com