练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （12分）用数学归纳法证明：
    ＝

    略

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：全优设计选修数学－2-2苏教版 苏教版 题型：047

    已知数列{an}的通项公式为an＝，数列{bn}的通项满足bn＝(1－a1)(1－a2)…－an)，用数学归纳法证明bn＝．

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修2－2)　2009－2010学年　第29期　总第185期 北师大课标 题型：013

    设数列{an}满足a1＝2，an+1＝2an＋2，用数学归纳法证明an＝4·2n－1－2的第二步中，设n＝k时结论成立，即ak＝4·2k－1－2，那么当n＝k＋1时，ak+1为

    [　　]
    A．

    4·2k－2

    B．

    4·2k+1－2

    C．

    4·2k－1－2

    D．

    4·2k+2－2

    查看答案和解析>>

    科目：高中数学 来源：2013届甘肃省高二4月月考（期中）数学试卷（解析版） 题型：选择题

    用数学归纳法证明“(n＋1)(n＋2)·…·(n＋n)＝2n·1·3·…·(2n－1)”，从“k到k＋1”左端需增乘的代数式为(　  )

    A．2k＋1　　　　　　B．2(2k＋1)         C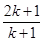．            D．.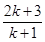

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设数列{an}满足a1＝2，an+1＝2an+2，用数学归纳法证明an＝4·2n-1-2的第二步中，设n＝k时结论成立，即ak＝4·2k-1-2，那么当n＝k+1时，ak+1为


    1. A.
      4·2k-2
    2. B.
      4·2k+1-2
    3. C.
      4·2k-1-2
    4. D.
      4·2k+2-2

    查看答案和解析>>

    同步练习册答案