
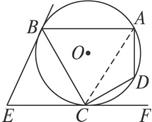
图2-1
思路分析:要求∠A,可转化为求∠BCD.由已知∠DCF的度数,想到先求∠ECB的度数,从而注意到题目所给的EB、EC为切线,将∠ECB与∠E的度数联系起来.
解法一:∵EB、EC是⊙O的切线,
∴EC=EB.又∠E=46°,
∴∠ECB=![]() =67°.
=67°.
∵∠DCF=32°,∴∠BCD=180°-67°-32°=81°.
∵∠A+∠BCD=180°,
∴∠A=180°-81°=99°.
温馨提示
本解法借助切线长定理和圆内接四边形的有关性质,此题还可借助于弦切角定理来求.
解法二:连结AC,∵EB、EC是⊙O切线,

图2-2
∴EB=EC.
∴∠ECB=![]() =67°.
=67°.
∵EF切⊙O于点C,∴∠BAC=∠ECB=67°,∠CAD=∠DCF=32°.
∴∠BAD=∠BAC+∠DAC=67°+32°=99°.
答案:99°


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
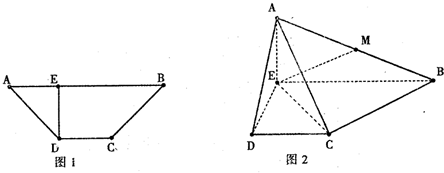 已知四边形ABCD是等腰梯形,AB=3,DC=1,∠BAD=45°,DE⊥AB,(如图1).现将△ADE沿DE折起,使得AE⊥EB(如图2),连结AC、AB,设M是AB的中点.
已知四边形ABCD是等腰梯形,AB=3,DC=1,∠BAD=45°,DE⊥AB,(如图1).现将△ADE沿DE折起,使得AE⊥EB(如图2),连结AC、AB,设M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
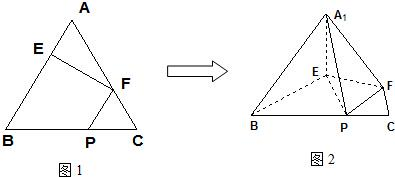
 如图l,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图2,将△ABE沿AE折起,使二面角B-AE-C成直二面角,连接BC,BD,P是棱BC的中点.
如图l,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图2,将△ABE沿AE折起,使二面角B-AE-C成直二面角,连接BC,BD,P是棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
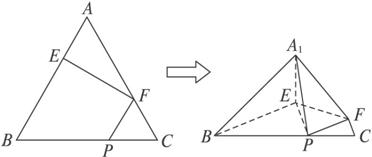
(1)求证:A1E⊥平面BEP;
(2)求直线A1E与平面A1BP所成角的大小;
(3)求二面角B-A1P-F的大小(用反三角函数值表示).
(1) (2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com